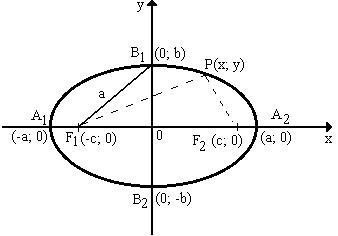3. Elipse
3.1.
Definição
Dados dois pontos fixos F1 e F2 de um plano, tais que a distancia entre estes
pontos seja igual a 2c > 0, denomina-se elipse, à curva plana cuja
soma das distancias de cada um de seus pontos P à estes pontos fixos
F1 e F2 é igual a um valor constante 2a , onde a > c.
Assim é que temos por definição: PF1
+ PF2 = 2 a
Os pontos F1 e F2 são denominados focos
e a distancia F1F2 é conhecida com distancia
focal da elipse.
O quociente c/a é conhecido como excentricidade
da elipse. Como, por definição, a > c, podemos afirmar que
a excentricidade de uma elipse é um número positivo menor que
a unidade.
3.2. Equação reduzida da elipse
Seja
P(x, y) um ponto qualquer de uma elipse e sejam F1(c,0) e F2(-c,0) os
seus focos. Sendo 2.a o valor constante com c < a, como vimos acima,
podemos escrever PF1 + PF2 = 2.a
Observe
que x – (-c) = x + c. Com
bastante paciência e aplicando as propriedades corretas, a expressão
acima depois de desenvolvida e simplificada, chegará a:
|
|