4. Parábola
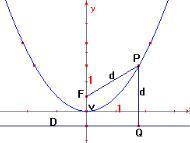
Dados um ponto F e uma reta D que não contenha F, o conjunto de pontos P = (x , y) que distam igual valor de F e de D é o que denomina-se uma parábola de foco F e diretriz D.
4.1. Equação
| Para
determinar a equação da parábola iniciamos escolhendo
um sistema de coordenadas conveniente de forma tal que: o foco F tem
coordenadas (0,f) ; a diretriz tem equação y = - f . d
( P , F ) = d ( P , Q ) x ² + y ² - 2fy + f ² = f ² + 2fy + y ² - 4fy = - x ² e portanto y = x ² / (4f ) e fazendo 1/ ( 4f ) = a obtemos y = a . x ² |
figura 1
|
4.2. Análise do coeficiente a
|
|
Na
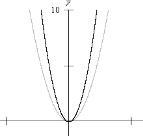
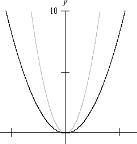
figura 2, temos a parábola y = x² e em preto
a parábola de equação y=a.x², com a > 1. |
Com está análise de gráficos, vemos que é o valor do coeficiente a que determina o quão fechada ou aberta é a parábola, e também se é uma parábola voltada para cima ou para baixo. No caso em que a < 0, obtemos para gráfico de y = a . x² a parábola representada na figura 4. |
figura 4 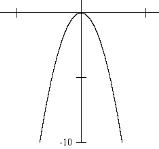
|
4.3. Deslocamento vertical
O
efeito que uma parábola de equação y = a. x ²
sofre ao adicionarmos uma constante b a sua expressão, deixando-a
da forma y = a.x ² + b, chama-se deslocamento vertical. Veja uma animação???? |
figura 5 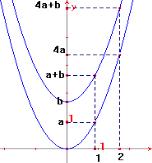 |
4.4. Desigualdades
A
relação de desigualdade y > a x² + b é satisfeita
pelos pontos P = (x, y) que estão na região cinza
na figura 6.
A relação de desigualdade y < a x² + b é satisfeita
pelos pontos P = (x, y) que estão na região cinza
na figura 7.
figura 6 |
figura 7 |