2.- Trigonometria na análise de SISTEMAS DINAMICOS
Obtenção de respostas naturais desses sistemas
Respostas naturais de um sistema dinâmico são as que dá quando não há excitação
ou input nenhum atuando sobre o mesmo. O exemplo clássico é o do oscilador harmônico
simples, quando oscila unicamente por suas características inerciais e elásticas, sem
sofrer a ação de nenhuma força externa.
O modelo matemático das oscilações naturais do oscilador harmônico simples
é a equação diferencial :
my" + ky = 0
onde m é sua massa, k sua constante elástica e y = y(t)
dá a elongação das oscilações em termos do tempo. Se as oscilações iniciam
de uma elongação inicial y(0) = y0 e com uma velocidade
inicial y'(0) = v0, então mostra-se que:

O uso das funções trigonométricas continua sendo essencial na análise de
sistemas dinâmicos mais complicados e que tenham comportamento oscilatório (
periódico, oscilatório amortecido ou oscilatório explosivo ). Esse tipo de análise
é fundamental na Engenharia, Física, Biomedicina, etc.
Obtenção de respostas excitadas desses sistemas
O que vamos dizer a seguir aplica-se ao caso dos sistemas dinâmicos
estáveis, que estão entre os de maior interesse nas aplicações na Engenharia. O
estável significa que todas as respostas naturais do sistema são
transitórias, ou seja : sua magnitude tende a zero ao tempo ir para o infinito.
Esses sistemas tem uma notável propriedade:
| basta sabermos o output do sistema quando excitado
por inputs senoidais para podermos achar seu output quando excitado por
QUALQUER input periódico |
Mais precisamente, quando excitados pelo input I = sen wt, eles produzem
um output da forma
y = R( w ) sen ( wt +  ( w ) ) ( w ) )
mais uma parcela transitória, que depende das condições iniciais do sistema,
mas que é irrelevante a longo prazo.
As funções R = R( w ) e
 = =  ( w ) podem ser achadas tanto
analiticamente como a nível de laboratório. Tendo-as, podemos usar o Teorema de
Fourier para obter a resposta ( output ) do sistema quando excitado por qualquer
input periódico de período fundamental T. Com efeito,
supondo o sistema também seja linear ( para que possamos dizer que o
output associado a uma soma é a soma dos inputs ), pelo tal teorema, o output será: ( w ) podem ser achadas tanto
analiticamente como a nível de laboratório. Tendo-as, podemos usar o Teorema de
Fourier para obter a resposta ( output ) do sistema quando excitado por qualquer
input periódico de período fundamental T. Com efeito,
supondo o sistema também seja linear ( para que possamos dizer que o
output associado a uma soma é a soma dos inputs ), pelo tal teorema, o output será:

| 

 / T ,
então ( sob condições que na prática sempre são verificadas e assim nem as explicitaremos )
esse sinal pode ser escrito como uma soma de senóides, chamada série de
Fourier :
/ T ,
então ( sob condições que na prática sempre são verificadas e assim nem as explicitaremos )
esse sinal pode ser escrito como uma soma de senóides, chamada série de
Fourier :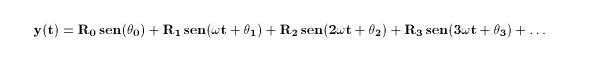

 ( w ) )
( w ) )