 |
o pai do bit |
 |
o pai do bit |
Claude Elwood Shannon nasceu nos USA em 1916. Formou-se em Matemática e Engenharia Elétrica na Universidade de Michigan, e fez seu mestrado e doutorado no MIT. Trabalhou a maior parte de sua vida nos Laboratórios Bell e, após uma rapidíssima vida de professor, aposentou-se com cerca de 50 anos. Até 2001, quando morreu, manteve-se intelectualmente ativo (poderíamos dizer que principalmente financeiramente, uma vez que dedicou-se a desenvolver programas de análise do sistema financeiro de Wall Street, com os quais acabou formando um imenso capital). Apesar de uma vida extremamente reclusa e estar afastado dos meios acadêmicos sempre foi motivo de muito rconhecimento, principalmente na comunidade dos engenheiros. Este pequeno texto objetiva dar uma idéia da razão dessa fama.
Motivado por necessidades de cálculos militares em balística, o Prof. Bush do MIT
construiu em 1930 um potentíssimo computador analógico eletromecânico: o
analisador diferencial de Bush. Na época era o computador mais potente em existência
no mundo. Contudo, como todo computador analógico, era uma máquina capaz de
resolver um único tipo de problema, no caso: equações diferenciais.
Apesar disso, tinha duas inovações que mais tarde foram decisivas para a invenção
dos computadores eletrônicos digitais: usava componentes eletrônicos e
tinha certa capacidade de programação (era capaz de resolver qualquer equação
diferencial dada, desde que suas componentes fossem reconfiguradas correspondentemente).
Nessa época, Shannon trabalhava como assistente de Bush e este sugeriu-lhe que
tentasse fazer um estudo matemático procurando descobrir o princípio que possibilitava
o funcionamento de sua máquina, construída um tanto quanto empiricamente.
Dedicando-se ao problema, Shannon descobriu que os circuítos baseados em relays
tinham seus estados de ON e OFF ( ie, de ligado e desligado ) regidos pelas
leis da Algebra de Boole. Mais do que isso, fazendo as associações:
foi capaz de mostrar como construir circuítos baseados em relays e capazes de
realizar cada uma das quatro operações aritméticas.
Hoje, em plena Era da Informática, poucas pessoas são capazes de se dar conta
de quanto enraizado estava o sistema de numeração decimal na mente dos engenheiros
da época. Shannon, além de provar a possibilidade de se construir um computador
totalmente eletrônico, foi o primeiro a atinar que os respectivos circuítos ficavam muito
mais simples (e mais baratos) com o abandono do sistema decimal em favor do sistema
binário.
Após a Segunda Guerra começaram a se multiplicar as tecnologias de transferência
de informação. Contudo, não havia uma teoria que fosse capaz de quantificar a
quantidade de informação que a ser transportada. Por exemplo, os engenheiros
de então achavam que seria apenas uma questão de progresso tecnológico se
conseguir transmitir mensagens telegráficas com maior velocidade do que se
podia fazer na época. Shannon ( em 1948 ) criou uma teoria, hoje fundamental
no trabalho cotidiano em Engenharia
de Comunicações e chamada Teoria da Informação, que mostrou que cada canal
de comunicações (seja ele um fio telegráfico, fio telefônico, cabo axial ou etc.)
tem uma velocidade limite característica.
Por exemplo, cada linha telefônica permite transmitir dados até uma certa
velocidade de transmissão. Se precisarmos usar uma velocidade maior teremos de
usar um canal de maior velocidade limite, por exemplo um cabo de fibras ópticas.
Se insistirmos usar a linha telefônica em velocidades maiores do que seu limite
teremos uma transmissão cada vez mais poluída por erros. Hoje, esse fenômeno é
até facilmente constatável por qualquer um que use seu microcomputador e modem
para fins de comunicação.
A Teoria de Informação que Shannon construiu, contudo, transcende em muito as
aplicações em comunicações. Shannon mostrou que aos elementos clássicos do trabalho
científico, massa e energia, precisamos acrescentar um terceiro: a
informação.
Mais do que isso, usando a Teoria das Probabilidades, Shannon
mostrou como medir a quantidade de informação. Sempre dando preferência
ao sistema de numeração binário, introduziu a unidade de medida de informação:
o bit : binary
digit.
Dizemos que recebemos um bit de informação quando ficamos sabendo qual, dentre
duas alternativas equiprováveis, a que efetivamente ocorreu.
Por exemplo:
recebemos um bit de informação quando soubermos qual o resultado do lance de
uma moeda, não viciada.
No instante que os cientistas passaram a ter condições de medir não apenas massa e energia mas também a informação iniciaram a investigar uma gama enorme de novos fenômenos nas ciências biológicas, sociais, etc. Por sua vez, os engenheiros puderam desenvolver uma grande quantidade de novas tecnologias de comunicações.
Embora a teoria de Shannon seja bastante técnica, vejamos um exemplo da utilidade que
tem tal unidade de informação. Voltemos ao problema que motivou os estudos de
Shannon: o problema da capacidade de comunicação de um canal transmissor.
A solução do problema é resumida numa fórmula, hoje básica da Teoria da Informação,
a chamada fórmula de Shannon:
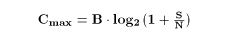
ela dá a velocidade máxima Cmax (em bits por segundo) com que sinais de potência S watts podem passar por um canal de comunicação, o qual deixa passar sem distorção apenas os sinais de frequência até B hertz, e que produz ruídos de potência no máximo N watts (e esses ruídos são do tipo usual, chamado ruído branco).
Vejamos um exemplo numérico importante: o caso das linhas telefônicas analógicas, essas que comumente encontramos aqui no Brasil. Elas são construídas para passar voz humana, frequência de até 3 400 hertz. Consequentemente:
Dá para V. começar a entender as limitações do modem ligado em seu computador?

