3.- O Início das aplicações da Trigonometria na Geodésia : W. Snell c. 1 600
A fim de obter coordenadas dos pontos de uma região na superfície da Terra,
Snell, que é mais conhecido pela lei da refração, introduziu a idéia de
triangulação. Essa consiste no seguinte:
- cobrimos a região com uma cadeia de triângulos de vértices A, B, C, etc
escolhidos de modo que cada um, C por exemplo, seja visível desde os dois
precedentes ( A e B no exemplo ) e dos dois seguintes ( D e E no exemplo). Tipicamente
esses vértices são escolhidos em topos de montanhas, torres de igrejas e
outros pontos de fácil visualização.
- medimos com exatidão o comprimento do lado AB, que é chamado base e
que preferivelmente deve estar sobre um terreno plano para facilitar as medidas
- medimos todos os ângulos dos triângulos da cadeia
- a partir da lei dos senos e da base e ângulos medidos, calculamos o
comprimento de todos os lados dos triângulos da cadeia
- usando-se Astronomia, calculamos as coordenadas ( latitude e longitude )
de um dos vértices e medimos o
ângulo ( chamado azimute ) que um dos lados faz com a direção norte.
Com todas essas informações, calculamos as coordenadas dos demais vértices.
Se a região tiver um diâmetro de até cerca de 20 Km, podemos considerar os
triângulos da cadeia como planos, e dizemos que temos uma triangulação
topográfica. Para regiões maiores precisamos levar em conta a esfericidade
da Terra, tratando os triângulos da cadeia como triângulos esféricos e dizemos
que temos uma triangulação geodésica. Esses dois tipos de triangulações
são os usados, respectivamente, pela Topografia e Geodésia.
Foi só a partir de cerca de 1 750 que começou a se tornar coisa comum se usar triangulações
geodésicas para a feitura de mapas de municípios, estados a até continentes, e
a se usar as triangulações topográficas para o mapeamento de áreas menores (diâmetro
menor do que 20 Km). Até então o uso das triangulações se restringia a trabalhos
de natureza mais científica do que técnica. Com efeito, os primeiros usos das
triangulações ocorreu
na determinação do comprimento de um
arco de meridiano para assim obter o tamanho da Terra.
A primeira dessas medidas de meridiano foi feita pelo próprio Snell, o qual
usou uma pequena modificação da versão clássica de triangulação, descrita
acima. Expliquemô-la com o exemplo da
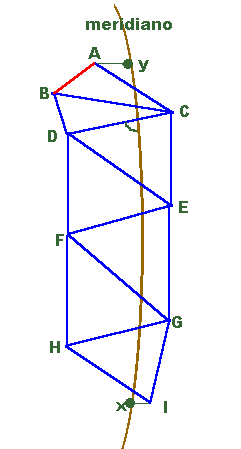
figura ao lado, que usa uma cadeia de 7 triângulos :
A base é AB e CD é o lado do qual medimos o azimute. Após calcular os lados
dos triângulos da cadeia, um novo uso de Trigonometria Esférica nos dá o
comprimento das projeções desses lados sobre o meridiano e isso nos permite
obter o comprimento do arco xy em Km. Tendo determinado a latitude dos
vértices extremos, A e I, temos a amplitude de xy em graus. Daí, um
cálculo simples nos dá quantos Km mede um arco de um grau na superfície
terrestre e então a circunferência da Terra.
Snell usou uma cadeia de 33 triângulos e
acabou fazendo um erro de 3.4%, para menos. Em 1 669, Picard usou uma cadeia
de 13 triângulos para refazer a medida do meridiano. Obteve para diâmetro
da Terra 12 554 Km, o que dá erro de 1.6%.
|


