|
1.- OS TRIANGULOS ESFERICOS
A idéia de triângulo esférico
Corresponde à idéia de triângulo desenhado em esferas, como é o caso da
Esfera Celeste ( o raio dessas esferas não interessa, como ficará claro
mais tarde ). Como definir isso corretamente ?
Se quizermos estender a noção de "triângulo" não apenas para
esferas mas para cones, cilindros e qualquer outra superfície,
obviamente, a primeira coisa a fazer é examinarmos um pouco mais
criticamente as características do familiar triângulo plano. É
fácil atinarmos que trata-se de uma figura contornada por trés
segmentos de reta ( chamados lados ) que encontram-se nas
extremidades ( os chamados vértices ).
Para levar essa noção para outras superfícies é só descobrir o que, na
superfície, faz o papel de segmento de reta. Um pouco de pensar nos faz
rapidamente ver que os "lados" devem ser as geodésicas
da superfície ( ou seja, linhas de comprimento mínimo sobre a
superfície ) unindo os "vértices".
Como fica isso tudo no caso objetivo, o dos triângulos esféricos? Bem,
é só atinar que:
na esfera, as geodésicas são arcos de círculos maximais
( ou seja, arcos de círculos que estão num plano passando pelo
centro da esfera ). |
Definição formal de triângulo esférico
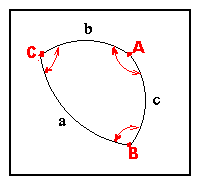
Dados três pontos A, B, C de uma esfera ( os quais não estão sobre um
mesmo círculo maximal ), o TRIANGULO ESFERICO de vértices
A, B e C é a figura da esfera contornada pelos três arcos maximais que
vão de A a B, de B a C e de C a A. Esses arcos maximais são chamados de
lados do triângulo.
Prova-se que quaisquer três pontos sobre uma esfera, os quais não estão
num mesmo círculo maximal, determinam um e só um triângulo esférico. É
de se obervar que a proibição dos vértices não estarem num mesmo
círculo maximal é semelhante à proibição, no caso de triângulos planos,
dos três vértices não estarem numa mesma reta. Mas ela também proibe a
possibilidade de um par de vértices serem diametralmente opostos (
poderíamos ver tais vértices como polos e o meridiano que passaria pelo
terceiro ponto seria um círculo maximal possuindo os três vértices ).
Isso equivale a dizer, conforme definição abaixo, que a medida de uma
lado de triângulo esférico nunca pode atingir valores iguais ou
superiores a 180 graus.
MEDIDA DE LADO de um triângulo esférico é a medida do ângulo que
ele subentende no respectivo círculo maximal. Ela, naturalmente, é
expressa em graus ou radianos, em vez de o ser em metros.
MEDIDA DO ANGULO EM UM VERTICE V de um triângulo esférico
é a medida do ângulo plano formado pelas tangentes em V a cada
um dos lados por V.
|

