FUNÇÕES DE BESSEL
A equação de Bessel de índice  é a EDO
onde
é a EDO
onde  é um número real.
é um número real.
O ponto  é um ponto singular regular para a
equação de Bessel. Aplicando, então, o método de Frobenius,
procuramos uma solução da forma
é um ponto singular regular para a
equação de Bessel. Aplicando, então, o método de Frobenius,
procuramos uma solução da forma
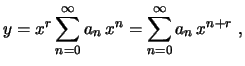
com

Substituindo na equação de Bessel, obtemos
Juntando o 1
 , o 2
, o 2
 e o
4
e o
4
 somatórios, obtemos
No segundo somatório acima, fazendo
somatórios, obtemos
No segundo somatório acima, fazendo  e fatorando o
coeficiente do primeiro somatório, obtemos
No segundo somatório, substituindo o índice
e fatorando o
coeficiente do primeiro somatório, obtemos
No segundo somatório, substituindo o índice  por
por  ,
separando os dois primeiros termos do primeiro somatório, obtemos
Como
,
separando os dois primeiros termos do primeiro somatório, obtemos
Como
 , segue que
, segue que
A equação (1) é a equação indicial. Suas raízes são
 e
e
 .
.
1
 Solução: Para
Solução: Para
 , a equação (2) se torna
ou seja,
, a equação (2) se torna
ou seja,
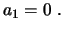 |
(4) |
A fórmula de recorrência (3) se torna
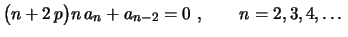 |
(5) |
De (5) segue que
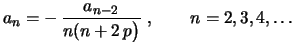 |
(6) |
Usando (4) e (6) e deixando para escolher mais tarde o valor de
 , obtemos
Temos
Em geral,
, obtemos
Temos
Em geral,
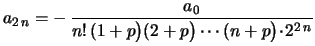 |
(7) |
Costuma-se fazer a escolha
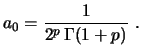 |
(8) |
Utilizando repetidas vezes a identidade
temos
Portanto com a escolha (8), (7) se torna
Obtemos, finalmente, a solução
Esta função é chamada de função de Bessel de
1
 espécie de índice
espécie de índice  e denotada por
e denotada por
 :
Para
:
Para
 Em particular,
Em particular,
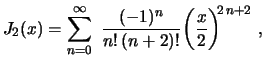
etc.

Examinando a expresão
vemos que  é uma função par, pois só envolve
potências de
é uma função par, pois só envolve
potências de  com expoentes pares e satisfaz
com expoentes pares e satisfaz  .
.
Abaixo mostramos o gráfico da função de
Bessel  mmostrando junto, pontilhadas, as funções
mmostrando junto, pontilhadas, as funções
e

para mostrar como o amplitude da função de Bessel é
compará com a destas funções.
O gráfico abaixo mostra em vermelho a função
 ,
em azul a função
,
em azul a função  e
em preto a função
e
em preto a função  .
.
Obs: A equação de Bessel não muda se
substituirmos  por
por  . Conseqüentemente
. Conseqüentemente  e
e  são duas soluções da equação de Bessel de índice
são duas soluções da equação de Bessel de índice  .
Precisamos investigar em que casos estas duas funções são
linearmente independentes.
.
Precisamos investigar em que casos estas duas funções são
linearmente independentes.
Exemplo: Vamos obter as expansões em séries de
potências das funções de Bessel
 e
e
 .
Note que, utilizando repetidas vezes a identidade
.
Note que, utilizando repetidas vezes a identidade
 ,
e, sabendo que
,
e, sabendo que
 , obtemos
isto é,
Logo
Levando em conta que
temos
e, finalmente,
, obtemos
isto é,
Logo
Levando em conta que
temos
e, finalmente,
Analogamente mostra-se que
Conclusão: Para
 ,
as funções de Bessel
,
as funções de Bessel
 e
e
 se expressam em termos de funções
elementeres,
se expressam em termos de funções
elementeres,
 e
e
 e são duas soluções linearmente independentes da
equação de Bessel de índice
e são duas soluções linearmente independentes da
equação de Bessel de índice

Mais geralmente, temos a seguinte
Propriedade: Se  não é um inteiro, então
não é um inteiro, então
 e
e  são duas soluções linearmente
independentes da equação de Bessel de índice
são duas soluções linearmente
independentes da equação de Bessel de índice  .
.
De fato, o
comportamento destas funções próximo ao ponto  é
dado pelo primeiro termo da série
Logo uma não é múltipla da outra e, portanto, são linearmente
independentes.
é
dado pelo primeiro termo da série
Logo uma não é múltipla da outra e, portanto, são linearmente
independentes.
Exemplo: Vamos mostrar que
 . Temos
Levando em conta que
temos que os 3 primeiros termos da série são nulos e o somatório
pode ser começado em
. Temos
Levando em conta que
temos que os 3 primeiros termos da série são nulos e o somatório
pode ser começado em  ,
ou, para
,
ou, para  ,
Usando o mesmo argumento prova-se a
,
Usando o mesmo argumento prova-se a
Propriedade: Para
 ,
,
Em resumo, provamos que:
- (i)
- Se
 não é um inteiro, então
não é um inteiro, então
 e
e  são duas soluções linearmente
independentes da equação de Bessel de índice
são duas soluções linearmente
independentes da equação de Bessel de índice  ;
;
- (ii)
- Se
 , então
, então  e
e
 são linearmente dependentes, mais precisamente,
são linearmente dependentes, mais precisamente,
 .
.
Para
 precisamos encontrar uma segunda
solução, linearmente independente de
precisamos encontrar uma segunda
solução, linearmente independente de  . Qualquer
solução da equação de Bessel de índice
. Qualquer
solução da equação de Bessel de índice  , linearmente
independente de
, linearmente
independente de  , é dita uma função de Bessel de
segunda espécie de índice
, é dita uma função de Bessel de
segunda espécie de índice  .
.
Para  , a equação de Bessel é
Uma solução é
, a equação de Bessel é
Uma solução é
 . Sabemos que podemos encontrar
uma solução, linearmente independente da forma
Substituindo na equação de Bessel,
que se reduz à primeira ordem fazendo
. Sabemos que podemos encontrar
uma solução, linearmente independente da forma
Substituindo na equação de Bessel,
que se reduz à primeira ordem fazendo  ,
Separando as variáveis e integrando,
ou
Escolhendo
,
Separando as variáveis e integrando,
ou
Escolhendo  e
e  ,
Por outro lado, de
segue que
Queremos encontrar a expansão de
,
Por outro lado, de
segue que
Queremos encontrar a expansão de
 . Como
. Como
 só
envolve potências de
só
envolve potências de  com expoente par, o mesmo acontece com seu
inverso.
Devemos ter
ou, efetuando a multiplicação,
Da igualdade das séries, temos
Segue que
com expoente par, o mesmo acontece com seu
inverso.
Devemos ter
ou, efetuando a multiplicação,
Da igualdade das séries, temos
Segue que

etc.

Logo
Finalmente,
Note que
Obtemos finalmente uma segunda solução para a eaquação de
Bessel de índice 0, que é linearmente independente de  ,
a função
conhecida como função de Bessel de Neumann de segunda
espécie de índice 0. Como
,
a função
conhecida como função de Bessel de Neumann de segunda
espécie de índice 0. Como
 , temos que
Conclusão: As únicas soluções da equação de
Bessel de índice 0 que são limitadas em intervalos do tipo
, temos que
Conclusão: As únicas soluções da equação de
Bessel de índice 0 que são limitadas em intervalos do tipo  são as da forma
são as da forma
Para
 porva-se a mesma conclusão e,
portanto, vale a seguinte
porva-se a mesma conclusão e,
portanto, vale a seguinte
Propriedade: As únicas soluções da
equação de Bessel de índice
 que são
limitadas em intervalos do tipo
que são
limitadas em intervalos do tipo
 são as da forma
são as da forma
A seguir mostramos em mesmo gráfico as funções
 e
e  , a primeira
representada por uma linha vermelha e a segunda por uma linha azul.
, a primeira
representada por uma linha vermelha e a segunda por uma linha azul.
Eduardo Brietzke
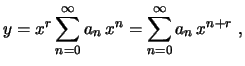 com
com 




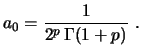





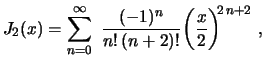 etc.
etc.
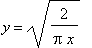 e
e


 e
em preto a função
e
em preto a função  .
.


 , obtemos
, obtemos







 ,
as funções de Bessel
,
as funções de Bessel
 e
e
 e são duas soluções linearmente independentes da
equação de Bessel de índice
e são duas soluções linearmente independentes da
equação de Bessel de índice

 e
e  quando
quando 



 não é um inteiro, então
não é um inteiro, então
 e
e  são duas soluções linearmente
independentes da equação de Bessel de índice
são duas soluções linearmente
independentes da equação de Bessel de índice  ;
;
 , então
, então  e
e
 são linearmente dependentes, mais precisamente,
são linearmente dependentes, mais precisamente,
 .
.








 . Como
. Como





 etc.
etc.




 , a primeira
representada por uma linha vermelha e a segunda por uma linha azul.
, a primeira
representada por uma linha vermelha e a segunda por uma linha azul.
