Séries de Fourier e Noções de Teoria Musical



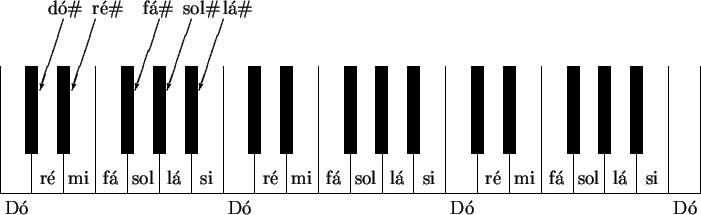
A figura abaixo representa um teclado. À medida que se avança para a direita, as notas vão ficando mais agudas. É fácil localizar as notas em um teclado. Note que as notas pretas se alternam em grupos de 2 e de 3 notas. Toda vez que tivermos um grupo de 2 notas pretas, a nota imediatamente anterior é um dó.


\begin{picture}(440,170) \par\put(0,30){\line(1,0){440}} \par\multiput(0,30)(20,... ...{2}{\line(0,1){55}} \par\multiput(360,55)(20,0){3}{\line(0,1){55}} \end{picture}

Entre o dó e o ré existe uma nota (preta no teclado), dó# (lê-se dó sustenido), que é mais aguda do que o dó, mas mais grave do que o ré.


O intervalo entre o dó e o dó# é de 1 semitom. Entre o dó# e o ré também é de 1 semitom, mas entre o dó e o ré é de 1 tom.


Note que entre o mi e o fá não existe nenhuma nota preta, portanto o intervalo é de 1 semitom. O intervalo si-dó também é de 1 semitom.


A escala de dó maior é a seqüência de notas: dó - ré - mi - fá - sol - lá - si - dó. Já a escala de ré maior, por exemplo, é a seqüência: ré - mi - fá# - sol - lá - si - dó# - ré. A escala de mi maior é: mi - fá# - sol# - lá - si - dó# - ré# - mi. Dependendo da escala que se considere, as notas que são sustenidas variam, o que não varia, o que é igual em todas as escalas são os intervalos entre as notas: - tom - tom - semitom - tom - tom - tom - semitom - . Isto ilustra o princípio de que o importante em música são os intervalos entre notas. Por exemplo, pegando uma melodia conhecida por todos, o parabéns a você, tocado de duas maneiras diferentes:


\begin{picture}(400,120) \par\put(0,40){\line(1,0){390}} \par\put(0,60){\line(1,... ...\char93 }} \par\put(338,47){\mbox{mi}} \par\put(368,47){\mbox{mi}} \end{picture}

Pode-se tocar seguindo as notas da segunda linha, ou então as da terceira linha. Nos dois casos a melodia será a mesma, apenas no segundo caso será um pouco mais aguda. Note que nas duas alternativas os intervalos são os mesmos. Por exemplo, o intervalo , seja ele sol-lá ou si-do#, nos dois caso é intervalo de 1 tom. O intervalo a-vo, em ambos os casos, sol-dó ou si-mi, é um intervalo de 2,5 tons. Uma mesma melodia pode ser transposta para os mais diversos tons, basta que sejam mantidos os intervalos entre as notas. Em outras palavras o que é realmente importante são os intervalos entre as notas.



Uma questão interessante é, por que se usam 12 notas (7 brancas + 5 pretas)? Quando se toca 2 ou mais notas ao mesmo tempo, dizemos que é um acorde. Alguns acordes são agradáveis ao nosso ouvido, isto é, são consonantes. Outros são desagradáveis, são dissonantes. Por que? Será que tudo isto é simplesmente uma questão de hábito, um produto de nossa cultura? Vamos ver que não. Existe uma explicação física. Vimos que uma corda fixa nos extremos, quando vibra, seu movimento é descrito por uma série

$\displaystyle u(x,t)=\sum_{n=1}^\infty \biggl(a_n\cos\frac{c\,n\,\pi\,t} {L}+b_n\,{\rm sen}\,\frac{c\,n\,\pi\,t}{L}\biggr)\,{\rm sen}\, \frac{n\,\pi\,x}{L} \ . $

Trata-se então da superposição de vários movimentos

$\displaystyle u_n(x,t)=\biggl(a_n\cos\frac{c\,n\,\pi\,t} {L}+b_n\,{\rm sen}\,\frac{c\,n\,\pi\,t}{L}\biggr)\,{\rm sen}\, \frac{n\,\pi\,x}{L} \ . $

Cada $ u_n(x,t)$ é periódico no tempo com período $ \displaystyle\,p_n=\frac{2\,L}{c\,n}\,$ e, portanto, freqüência $ \displaystyle\,f_n=\frac{c\,n}{2\,L}\,$. É importante notar que todas estas freqüências são múltiplas da mais baixa, a chamada freqüência fundamental. De fato,

$\displaystyle f_n=n\,f_1 \ . $

Em outras palavras, quando fazemos vibrar uma corda, o que ouvimos não é um som puro, mas sim a superposição de vários sons, cujas freqüências são todas elas múltiplas da freqüência fundamental. Na prática a freqüência fundamental é a que mais contribui, ou seja $ a_1$ e $ b_1$ predominam sobre os outros coeficientes. Quando falamos na freqüência de uma nota, estamos falando na freqüência fundamental. As vibrações de freqüência mais alta são os chamados harmônicos ou sobretons. O som do diapasão (o objeto usado como padrão de afinação) é desprovido dos harmônicos mais altos, soa só o tom fundamental. Por isto o diapasão produz um som pobre, sem beleza. Os harmônicos mais altos é que dão a riqueza ao som e a proporção com que eles entram é que produz o timbre característico de cada instrumento. Um mesmo dó tocado por um violino ou por uma flauta é a mesma nota, mas soa bastante diferente. Cada instrumento tem o seu timbre peculiar. Por exemplo, pode acontecer que num certo instrumento só os $ u_n$ para $ n$ ímpar soem e em outro instrumento não seja assim.



Consideremos o dó bem da esquerda do teclado da figura acima. Chamemos de $ \lambda$ a sua freqüência. Suponhamos que se trate do "dó da fechadura" do piano, cuja freqüência é $ \lambda=264$ Hz. O próximo dó mais agudo terá freqüência $ 2\,\lambda$. E toda vez que este intervalo (chamado de oitava) se mantiver, a freqüência dobrará. Por exemplo, se um mi tiver uma certa freqüência $ \mu$, o próximo mi, uma oitava mais agudo, vai ter freqüência $ 2\,\mu$. Portanto o primeiro dó tem freqüência $ \lambda$, o segundo tem freqüência $ 2\,\lambda$, o terceiro $ 4\,\lambda$ e o quarto $ 8\,\lambda$. Todos eles soam junto no primeiro dó. São, respectivamente $ u_1(x,t)$, $ u_2(x,t)$, $ u_4(x,t)$ e $ u_8(x,t)$. Mas também soam junto com o primeiro dó, $ u_3(x,t)$ com freqüência $ 3\,\lambda$, $ u_5(x,t)$ com freqüência $ 5\,\lambda$, $ u_6(x,t)$ com freqüência $ 6\,\lambda$, etc? Que notas são estas?



A nota de freqüência $ 3\,\lambda$ deve situar-se entre o dó de freqüência $ 2\,\lambda$ e o dó de freqüência $ 4\,\lambda$. Resulta ser um sol, que está representado no teclado abaixo.


\begin{picture}(440,130) \par\put(0,30){\line(1,0){440}} \par\multiput(0,30)(20,... ...{2}{\line(0,1){55}} \par\multiput(360,55)(20,0){3}{\line(0,1){55}} \end{picture}

Lembrando que em um intervalo de 1 oitava a freqüência dobra, concluímos que a nota de freqüência $ 6\,\lambda$ é também um sol, também localizado no teclado da figura.



Qual será a nota de freqüência $ 5\,\lambda$? Deve ser uma nota quase a meio caminho entre o dó de freqüência $ 4\,\lambda$ e o sol de freqüência $ 6\,\lambda$. Na verdade é um mi, representado abaixo




\begin{picture}(440,130) \par\put(0,30){\line(1,0){440}} \par\multiput(0,30)(20,... ...{2}{\line(0,1){55}} \par\multiput(360,55)(20,0){3}{\line(0,1){55}} \end{picture}

Note que o mi-$ 5\lambda$ é a 4 $ ^{{\rm a}}$ nota depois do dó-$ 5\lambda$ e que o sol-$ 6\lambda$ é a 3 $ ^{{\rm a}}$ nota depois do mi-$ 5\lambda$. Está faltando ainda a 7 $ ^{{\rm a}}$ nota da série harmônica do dó. Acontece que esta 7 $ ^{{\rm a}}$ nota não é nenhum dos sons deste teclado, ela é dissonante em relação ao tom fundamental. Veremos em um problema de uma das listas de exercícios, que no caso da corda percutida, como no piano, pode-se conseguir que este 7 $ ^{{\rm o}}$ harmônico não soe, seja eliminado, bastando para isto que o martelo bata na corda em um ponto conveniente (veremos que este ponto conveniente é um nó do 7 $ ^{{\rm o}}$ harmônico; na prática os fabricantes de piano fazem com que o martelo bata na corda em um ponto que dista de uma das extremidade fixas da corda aproximadamente $ 1/7$ do comprimento da corda). Gostaríamos de frizar que todas as notas de freqüência $ \,\lambda\,$, $ \,2\,\lambda\,$, $ \,3\,\lambda\,$, $ \,4\,\lambda\,$, etc, soam junto (apenas com menor intensidade) quando se toca do dó de freqüência $ \,\lambda\,$.



Usando novamente que em um intervalo de 1 oitava a freqüência dobra, concluímos que a freqüência do 1 $ ^{{\rm o}}$ sol é a metade da freqüência do 2 $ ^{{\rm o}}$ sol, $ \frac{3}{2}\lambda$. podemos então completar um pouco mais nosso quadro de freqüências




\begin{picture}(440,130) \par\put(0,30){\line(1,0){440}} \par\multiput(0,30)(20,... ...{2}{\line(0,1){55}} \par\multiput(360,55)(20,0){3}{\line(0,1){55}} \end{picture}



Neste ponto uma simples inspeção nos mostra que em qualquer altura do teclado, se consideramos uma progressão dó-mi-sol, a razão entre suas freqüências é 4:5:6. Justamente, estas 3 notas tocadas em conjunto são bastante agradáveis ao ouvido, constituindo o acorde de dó maior. Portanto o acorde maior não é uma invenção da civilização ocidental. Ele não é agradável a nosso ouvido simplesmente porque já estamos habituados a ouvi-lo. Existe uma razão muito mais forte, de natureza física para que o acorde maior seja agradável ao ouvido. É que a razão entre as freqüências das notas que o compõem são razões entre números inteiros pequenos, no caso 4:5:6.



Para completar um pouco mais nosso quadro de freqüências, usamos que o acorde de fá maior é fá-lá-dó. (se duvidar disto, note que o intervalo fá-lá é de 2 tons, exatamente como o 1 $ ^{{\rm o}}$ intervalo dó-mi do acorde de dó maior e o intervalo lá-dó é de 1,5 tons, exatamente o mesmo que mi-sol). Segue que a razão entre as freqüências de fá-lá-dó é 4:5:6. Considerando o dó- $ 2\,\lambda$, temos que o lá a sua esquerda tem freqüência

$\displaystyle \frac{5}{6}\,2\,\lambda=\frac{5}{3}\,\lambda \ . $

Já o fá tem freqüência

$\displaystyle \frac{4}{6}\,2\,\lambda=\frac{4}{3}\,\lambda \ . $

Tomando múltiplos, obtemos as freqüências de todos os outros fá e lá do teclado.



Analogamente, começando em um sol e avançando 2 tons para à direita e depois mais 1,5 tons, concluímos que o acorde de sol maior é sol-si-ré. Portanto a razão entre as freqüências de sol-si-ré também é 4:5:6. Mas já conhecemos a freqüência da nota sol. Isto nos permite calcular as freqüências de si como sendo

$\displaystyle \frac{5}{4}\,\frac{3}{2}\,\lambda=\frac{15}{8}\,\lambda $

e de ré como

$\displaystyle \frac{6}{4}\,\frac{3}{2}\,\lambda=\frac{9}{4}\,\lambda \ . $

Com isto completamos as freqüências de todas as notas brancas do teclado.


\begin{picture}(310,130) \par\put(0,30){\line(1,0){300}} \par\multiput(0,30)(20,... ...{2}{\line(0,1){55}} \par\multiput(220,55)(20,0){3}{\line(0,1){55}} \end{picture}


As notas que, quando tocadas juntas, soam agradáveis ao ouvido, são aquelas tais que a razão entre suas freqüências são frações entre números inteiros pequenos. Por exemplo,


       - para ré-sol, obtemos a fração $ \frac{9}{8}\big/\frac{3}{2}=\frac{3}{4}$ e portanto são consonantes.


       - para fá-si, obtemos a fração $ \frac{4}{3}\big/\frac{15}{8}=\frac{32}{45}$ que tem numerador e denominador bastante grandes. Estas duas notas portanto são bastante dissonantes. Tocadas ao mesmo tempo soam bastante desagradáveis ao ouvido. Tocando ao mesmo tempo duas notas vizinhas, como dó e dó#, pode-se notar até um batimento, no entanto é fácil cantar a seqüência dó-dó#. Já para uma pessoa sem bom um treinamento musical é bem difícil cantar em seqüência fá-si, é quase impossível guardar este intervalo na memória.



A escala de dó maior que acabamos de construir é a chamada escala da intonação justa. Ela apresenta um sério inconveniente. As razões entre os intervalos de 1 tom não são sempre iguais. As razões entre as freqüências de dó-ré , fá-sol e lá-si são 9:8. As razões entre as freqüências de ré-mi e sol-lá são de 10:9. Este tipo de coisa e, mais ainda quando as notas pretas são consideradas, criou uma série de complicações. Sem querer entrar em problemas técnicos, vamos mencionar apenas que para enfrentar esta situação, era preciso, em lugar das 12 notas atuais, considerar mais de 30 notas, algumas delas diferindo tão pouco entre si, que só um ouvido treinado podia detectar a diferença.

Visando contornar esta dificuldade, os teóricos da música no século XVII propuseram a escala do igual tempreramento. Esta escala consiste em dividir a oitava em 12 notas de modo que a razão entre as freqüências de duas notas vizinhas (intevalo de 1/2 tom) é sempre a mesma. Consideremos todas as notas entre o dó-$ \lambda$ e o dó-$ 2\lambda$


dó - dó# - ré - ré# - mi - fá - fá# - sol - sol# - lá - lá# - si - dó


As freqüências destas notas são

$\displaystyle \lambda \ - \ \lambda\,\alpha \ - \ \lambda\,\alpha^2 \ - \ \lam... ...- \ \lambda\,\alpha^4 \ - \cdots\cdots \ - \lambda\,\alpha^{12}=2\,\lambda \ , $


de modo que $ \,\alpha=\sqrt[12]{2}\approx 1.0594\,$. Na escala do igual temperamento, para qualquer intervalo de 1 tom, a razão entre as freqüências é sempre $ \,\alpha^2\approx 1.1225\,$. É intressante comparar este valor com as duas possibilidade $ \,9/8=1.1250\,$ e $ \,10/11\approx 1.1111\,$, que observamos na escala da justa intonação. Existe uma pequena diferença entre as duas escalas. A escala do igual temperamento foi se impondo lentamente entre os séculos XVII e XVIII, tendo se consolidado definitivamente com o compositor J. S. Bach, que compôs o dois volumes do Cravo Bem Temperado, o primeiro deles em 1722 e o segundo em 1744. No sistema de justa intonação não era possível fazer música em todos os tons. Em cada um dos volumes do Cravo Bem Temperado, Bach compôs 24 prelúdios e 24 fugas, um conjunto para cada um dos 12 tons maiores e dos 12 tons menores, provando definitivamente que no sistema de igual temperamento pode-se fazer música em todos os tons.


Eduardo H. M. Brietzke 2001-12-14