Álgebra Linear Numérica

O planejamento e a análise de um sistema linear de controle consiste nas tarefas básicas seguintes:

(i)

testar a controlabilidade, observabilidade, estabilidade e propriedades relacionadas;

(ii)

estabilizar o sistema usando realimentação , se o sistema original não é estável ou possui frequências naturais indesejadas;

(iii)

ajustar o comportamento do sistema usando realimentação de maneira que determinados critérios são alcançados (reajuste de pólos, otimização quadrática)

(iv)

assegurar a estabilidade sob perturbações (estabilização robusta), sejam elas estruturadas ou não , usando otimização nos espaços $H_{\infty}$ e $H_2$;

(v)

estimar as variáveis de estado usando observadores;

(vi)

construir modelos correspondentes de ordem reduzida que ainda possuem certas propriedades estruturais (redução de modelo), dessa forma viabilizando a análise de estruturas muito grandes;

(vii)

identificar as matrizes que representam o sistema na formulação via variáveis de estado através do uso de dados experimentais.

Essas tarefas dão origem a muitas tarefas interessantes no campo da Álgebra Linear. As mais importantes são : solução de equações matriciais (Lyapunov, Sylvester, Riccati algébrica e do Observador de Sylvester), cálculo computacional de normas de funções matriciais (normas $H_2$ e $H_{\infty}$), solução de problemas estruturados de autovalores, valores singulares e valores singulares generalizados, entre outros.

As equações de Lyapunov

$$\begin{array}{c} A X + X A^T = C \\ A X A^T - X = C \end{array}$$

aparecem na análise de estabilidade, computação da norma $H_2$, redução de modelo e outras aplicações de sistemas contínuos e discretos, respectivamente.

A equação de Sylvester $A X + X B = C$ (caso de um sistema contínuo) aparece na redução em blocos de uma matriz $A$ ou também no cálculo da projeção estável com respeito a uma região especificada do plano complexo.

A equação do Observador de Sylvester

$$X A - F X = G C$$

onde as matrizes $A$ e $C$ são dadas e $X, F$ e $G$ são incógnitas, aparece na estimação dos estados de um sistema clássico observável de primeira ordem. Similarmente, aparece a equação do Observador de Sylvester para sistemas generalizados de primeira ordem,

$$X A - F X E = G C$$.

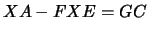
A equação algébrica de Riccati para um sistema contínuo escreve-se

$$X A + A^T X - X B R^{-1} B^T X + Q = 0 ,$$

enquanto a equação algébrica de Riccati para aquele sistema escreve-se

$$A^T X A - A^T X B(R + B^T X B)^{-1} B^T X A + Q = X.$$

Essas duas equações , e suas extensões , aparecem no problema do regulador linear quadrático (LQR), no problema do regulador linear Gaussiano (LQG) e no problema de otimizacao em $H_{\infty}$.