


Next: About this document ...
Dadas matrizes
onde (equação de compatibilidade)
calcularemos matrizes 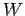 e
e 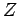 , juntamente com
matrizes diagonais
, juntamente com
matrizes diagonais 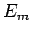 ,
, 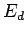 , e
, e 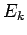 , tais que
as matrizes do modelo simétrico
, tais que
as matrizes do modelo simétrico
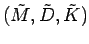 ,
dadas por
satisfazem a equação de atualização
e a equação de invariância do espectro não -medido
onde
,
dadas por
satisfazem a equação de atualização
e a equação de invariância do espectro não -medido
onde
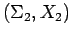 representa qualquer conjunto (desconhecido) de
pares do tipo frequência - modo de vibração não incluídos na
atualização .
representa qualquer conjunto (desconhecido) de
pares do tipo frequência - modo de vibração não incluídos na
atualização .
Aqui disponibilizamos programa para o cálculo do conjunto de
parâmetros de ajuste
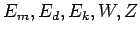 . Uma vez estabelecidos
os dados de entrada correspondendo as matrizes
. Uma vez estabelecidos
os dados de entrada correspondendo as matrizes 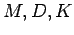 ,
, 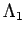 e
e 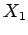 , a quantidade
, a quantidade
é primeiramente calculada, para validação da equação de
compatibilidade.
Joao Carvalho
2005-08-16
![$\displaystyle \Lambda_1 = \left[
\begin{array}{cccc}
\lambda_1 & & & \\
& \lambda_2 & & \\
& & \dots & \\
& & & \lambda_r \end{array} \right] , $](img1.gif)
![$\displaystyle \Lambda_1 = \left[
\begin{array}{cccc}
\lambda_1 & & & \\
& \lambda_2 & & \\
& & \dots & \\
& & & \lambda_r \end{array} \right] , $](img1.gif)
![$\displaystyle \Sigma_1 = \left[
\begin{array}{cccc}
\mu_1 & & & \\
& \mu_2 & & \\
& & \dots & \\
& & & \mu_r \end{array} \right] , $](img2.gif)
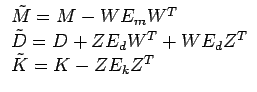
![]() . Uma vez estabelecidos
os dados de entrada correspondendo as matrizes
. Uma vez estabelecidos
os dados de entrada correspondendo as matrizes ![]() ,
, ![]() e
e ![]() , a quantidade
, a quantidade