Elisa Friedrich Martins *
Nicolau Matiel Lunardi Diehl *
Maria Alice Gravina *
Curso de Licenciatura em Matemática da UFRGS
|
 |
||||
|
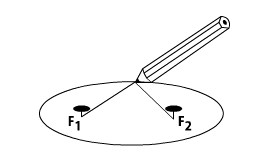
1)
Clicando no botão 2) Para
começar a animação e
desenhar a elipse escolhida dê um click
neste botão ATENÇÃO: a animação só vai funcionar se o ponto A2 estiver entre os quadradinhos verdes no segmento K. Para posicioná-lo corretamente clique no 1º botão. |
|
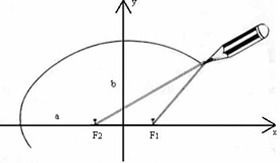
Iremos deduzir a equação da elipse utilizando-se do Teorema de Pitágoras. Vamos indicar por 2a a constante aludida na definição de elipse. Tomemos o sistema de cordenadas X, Y como na figura ao lado. Neste caso F1 = (-c,0), F2 = (c,0). Sendo P = (x,y) um ponto da elipse, devemos ter d(P,F1) + d(P,F2) = 2a, ou seja, |
 |
Lembrando que a²
= b² + c² resulta b²x²
+ a²y² = a²b², e dividindo a equação por a²b², temos |
|
|
Para manipular o instrumento, prossiga da seguinte forma:
|
|
O
instrumento, chamado "Biellismo del Delaunay", foi tirado do site
http://www.museo.unimo.it/theatrum/macchine/_00the.htm
e construído com o programa Régua e Compasso. |
|
|
Seja
b = |
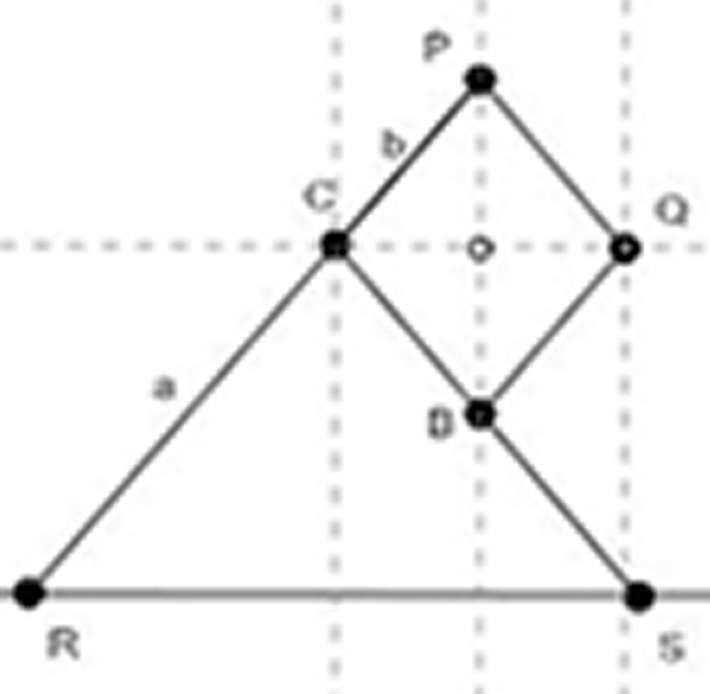 |
A
semelhança dos triângulos RPP' e RCC',
nos dá a seguinte
relação: |
Comparando
as equação da elipse com a resultante do "instrumento que desenha curva " podemos perceber que embora se pareça geometricamente, ela não é uma
elipse.
|
Elisa
Friedrich Martins é aluna da Licenciatura em Matemática-UFRGS.E-mail: titamat@yahoo.com.br
Nicolau Matiel Lunardi Diehl é aluno da Licenciatura em Matemática-UFRGS.E-mail: nicolaudiehl@yahoo.com.br
Maria Alice Gravina é professora do curso de Licenciatura em Matemática da
UFRGS, mestre em Matemática pelo IMPA-CNPq e aluna do programa de doutorado
em Informática na Educação-UFRGS
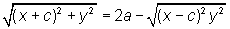 =>
=> 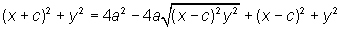 =>
=>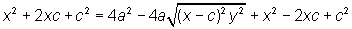 =>
=> 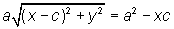 =>
=> 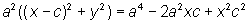 =>
=>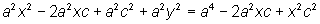 =>
=> 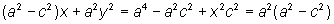
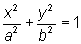
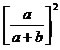 => x'-x
=
=> x'-x
= 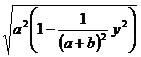 =
= 