Márcia Rodrigues Notare *
Maria Alice Gravina *
Curso de Licenciatura em Matemática da UFRGS
|
Nesta atividade
vamos construir, inicialmente, retângulos de mesmo perímetro
e observar o que acontece com a área ao mudar-se a forma do retângulo.
Depois vamos construir
retângulos de mesma área e, da mesma forma, observar o que
acontece com o perímetro.
Vamos utilizar
o software Cabri-Geometry que nos permite modificar as dimensões
do retângulo, a partir de deslocamento de vértices.
Como construir vários
retângulos de mesmo perímetro?
Para construir estes
retângulos, fixamos um certo valor para o perímetro, ou seja,
para a soma dos lados:
Perímetro
= 2a + 2b, com a e b lados do retângulo.
Fixar o perímetro
do retângulo significa manter fixa a soma dos lados a e b. Para isto,
vamos construir um segmento AB e um ponto C móvel sobre este segmento:
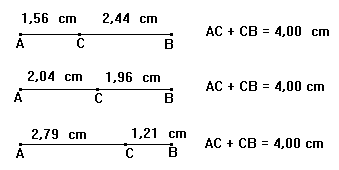
Se tomamos AC e
CB como lados do retângulo, teremos a soma de dois de seus lados
fixa e igual à AB e o perímetro fixo igual à 2*AB.
Ao movimentar o ponto C sobre AB obtemos diferentes medidas para os lados
do retângulo, conservando o perímetro fixo.
Vamos então
agora construir os retâgulos cujos lados são AC e AB:
-
A partir dos segmentos
AC e CB construídos acima, construa dois círculos concêntricos,
de raios AC e CB (utilize a ferramenta Compasso);
-
Construa o retângulo
sobre dois raios perpendiculares;
-
Calcule o perímetro
deste retângulo;
-
Movimente o ponto C
que está sobre o segmento AB construído inicialmente e observe
o que acontece.
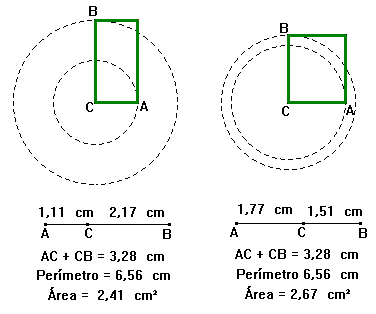
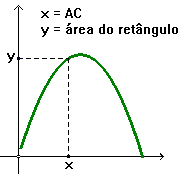
Observe a variação
da área do retângulo:
-
para C próximo
de A a área é quase zero
-
conforme C se afasta
de A a área vai aumentando
-
a área atinge
seu maior valor no quadrado
-
conforme C se aproxima
de B a área vai diminuindo
-
Como é "lei"desta
função ?
|
|
|
 |
Como construir diversos
retângulos de mesma área?
Para fixar um valor
de área do retângulo, precisamos fixar o produto de seus lados,
pois, como sabemos,
Área
= a . b, com a e b lados do retângulo
Mas como construir
geometricamente um produto constante?
Para isto vamos
usar o seguinte teorema:
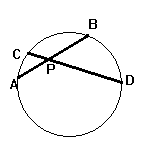
Se duas cordas
AB e CD de um círculo
se interceptam
em um ponto P, o produto
PA . PB é
igual ao produto PC . PD |
 |
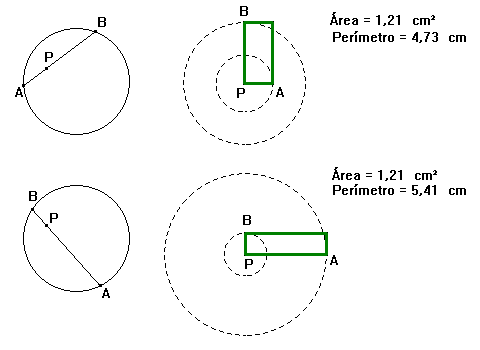
A partir deste teorema
podemos construir retângulos de mesma área. Basta seguir a
construção abaixo:
-
Construa uma circunferência
e um ponto P fixo em seu interior;
-
Construa um ponto A
sobre a circunferência;
-
Construa uma corda
AB passando pelo ponto P (construa inicialmente a reta AP e depois a corda)
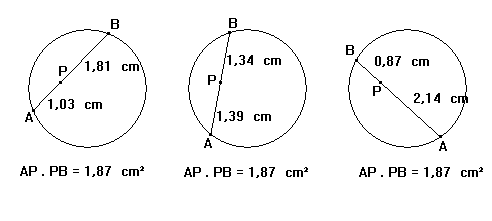 Podemos agora construir
o retângulo:
Podemos agora construir
o retângulo:
- Usando os segmentos
PA e PB construídos acima, construa dois círculos concêntricos
de raios PA e PB (utilize a ferramenta Compasso);
-
Construa o retângulo
sobre dois raios perpendiculares;
-
Calcule a área
deste retângulo;
-
Movimente o ponto A
construído sobre o círculo e observe o que acontece com a
área do retângulo construído.
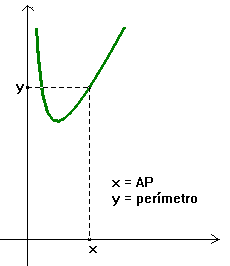
O gráfico
ao lado nos dá a varição do perímetro do retângulo
em
função
da distância de A à P. Algumas perguntas que podemos
nos colocar:
-
quando o perímetro
é mínimo ?
-
quando o perímetro
é máximo?
-
como é a "lei"
desta função ?
|
 |
Ao final desta atividade deve
ter se tornado claro que não existe relação funcional entre perímetro e área de retângulos.
Para os alunos isto nem sempre é claro,
o que se reflete quando fazem afirmações do tipo "se aumenta a área aumenta o perímetro"
ou o contrário "se aumenta o perímetro aumenta a área".
Conforme vimos:
Márcia Rodrigues Notare é licenciada em Matemática e mestranda em Informática na Educação, Instituto de Informática-UFRGS.
Maria Alice Gravina é professora do curso de Licenciatura em Matemática da UFRGS, mestre em Matemática pelo IMPA-CNPq e aluna
do programa de doutorado em Informática na Educação-UFRGS