Estudando Retas e Parábolas
com o Software Graphmática
Marina Menna Barreto * Maria Alice Gravina *
|
FAMILIARIZAÇÃO COM O SOFTWARE:

Em View temos a opção Graph Paper, que possibilita que se mude o "tipo de papel gráfico", podendo-se escolher a escala logaritmica, retangular, trigonométrica ou polar. Faça a escolha Rectangular e Dots.
Em Colors pode-se mudar a cor de fundo e as cores que serão desenhados os gráficos. Faça a escolha White e em Grid Elementes/Colors indique cores para os gráficos .
Em Grid Range pode-se mudar a escala das coordenadas. Na janela acima temos x entre -8 e 8 e para y entre -4 e 4.
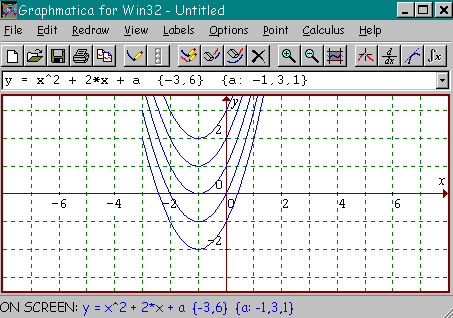
Vamos nos familiarizar também com a sintaxe usada no programa. Para indicar uma certa função precisamos usar a linguagem que o programa entende. Por exemplo, se queremos os gráficos das funções y= x2 + 2x +a ( "a" parâmetro variável ) devemos escrever:
y = x^2 + 2*x + a {-3,6} {a: -1,3,1}
Onde {-3,6}: indica como domínio da função o intervalo [ -3 , 6 ]
{a: -1, 3, 1}: indica " a" variando de -1 a 3 , de unidade em unidade.
ATENÇÃO: O programa só aceita a letra "a" para expressar o parâmetro.
Observe o exemplo a seguir:
ATIVIDADE 1: Movimento de Retas:1.1. Considere a função y = ax
- Faça o gráfico da função com a = 1
- Obtenha o gráfico da função para diferentes valores de "a" , positivos e negativos. Para isto utilize as instruções para a mudança de parâmetro mostrada acima.
- Qual o significado do parâmetro "a" nos gráficos obtidos? Associe o valor do parâmetro ao gráfico correspondente.
- Descreva os gráficos das funções em termos de movimentos aplicados ao gráfico de y = x
- Faça o gráfico da função com a = 0
- Obtenha o gráfico da função para diferentes valores de " a"
- Qual o significado do parâmetro " a " nos gráficos obtidos? Associe o valor do parâmetro ao gráfico correspondente
- Descreva os gráficos das funções em termos de movimentos aplicados ao gráfico de y = x
- simétricos em relação ao eixo OX
- simétricos em relação ao eixo OY
- paralelos
1.5. Usando relações algébricas podemos desenhar. Usando os recursos de domínio e parâmetro do programa, faça as figuras a seguir. Antes observe o exemplo abaixo:

ATIVIDADE 2: Movimento de Parábolas:2.1. Considere a função y = ax2
- Faça o gráfico da função com a = 1
- Obtenha o gráfico desta função para diferentes valores de "a", positivos, negativos e fracionários
- Qual o significado do parâmetro "a" nos gráficos obtidos? Descreva os gráficos das funções em termos de movimentos aplicados ao gráfico de y = x2
- Faça o gráfico da função com a = 1
- Obtenha o gráfico desta função para diferentes valores de "a", positivos, negativos e fracionários
- Qual o significado do parâmetro "a" nos gráficos obtidos? Descreva os gráficos das funções em termos de movimentos aplicados ao gráfico de y = x2
- Faça o gráfico da função com a = 1
- Obtenha o gráfico desta função para diferentes valores de "a", positivos, negativos e fracionários
- Qual o significado do parâmetro "a" nos gráficos obtidos? Descreva os gráficos das funções em termos de movimentos aplicados ao gráfico de y = x2
- Faça o gráfico da função para diferentes valores de " k", " m " e " n "
- Descreva os gráficos das funções em termos de movimentos aplicados ao gráfico de y = x2
- Qual a condição para que a parábola seja do tipo 'voltada para cima' ou 'voltada para baixo' ?
- Quais as coordenadas dos pontos de máximo / mínimo do gráfico ?
- Em que pontos o gráfico intercepta o eixo y ? e o eixo x ?
- Em que intervalos a função é crescente ? e decrescente ?
Obs.: A expressão geral de uma função do tipo parábola é y = A . x 2 + B . x + C . Para descrever o gráfico da função em termos de movimentos aplicados ao gráfico de y = x 2 é interessante escrever a função na forma y = k. (x + m ) 2 + n , e isto sempre é possível. Veja como se faz isto.
2.6. Obtenha a expressão da função correspondente a cada um dos gráficos descritos abaixo, em termos de movimentos sucessivos que iniciam no gráfico de y = x 2. Faça o gráfico da função e confira se a expressão fornece o gráfico solicitado.
- Faça o gráfico de y = 2 . x2 + 2 . x + 3
- Faça o gráfico de y = 2 . ( x +1/2 ) 2 + 5/2
O que se observa ?
- Descreva o gráfico de y = 2. x2 + 2. x + 3 em termos de movimentos aplicados ao gráfico de y=x2
- translação horizontal de duas unidades para a direita + translação vertical de 1 /2 para baixo
- dilatação de fator 2 + translação horizontal de 1 para à esquerda
- translação horizontal de 1 para a direita + reflexão em relação ao eixo y
- reflexão em relação ao eixo x + translação vertical de 5 / 3 para cima + dilatação de fator 2
- translação vertical de 1 unidade + reflexão em relação ao eixo x + contração de 1/2
Obs.: este estudo de gráficos através de movimentos aplicados ao gráfico de funções mais simples pode ser utilizado com diferentes famílias de funções. Por exemplo, dada a função y = x 3 , podemos rapidamente "enxergar" os gráficos das funções y = x 3 + a, y = ( x + a ) 3 , y = a . x 3 e mais geralmente y = k . ( x + m ) 3 + n
FUNÇÃO DO 2o GRAU ESCRITA NA FORMA CANÔNICA:Podemos mostrar que o gráfico f(x) = ax2 + bx + c pode ser obtido a partir de transformaçõe aplicadas ao gráfico y = x2 . Para isto são necessárias algumas transformações algébricas na expressão de f. Siga passo a passo as transformações abaixo:
Márcia Rodrigues Notare é licenciada em Matemática-UFRGS; mestranda em Informática na Educação, Instituto de Informática-UFRGS.E-mail:notare@inf.ufrgs.br
Marina Menna Barreto é licencianda em Matemática-UFRGS.E-mail:marina@mat.ufrgs.br
Maria Alice Gravina é professora do curso de Licenciatura em Matemática da UFRGS, mestre em Matemática pelo IMPA-CNPq e aluna do programa de doutorado em Informática na Educação-UFRGS.E-mail:gravina@mat.ufrgs.br