|
FÓRMULA
DA SOMA DOS TERMOS DE UMA PA FINITA
|
|
|
Observando a PA finita (1,
3, 5, 7, 9, 11, 13, 15) podemos destacar seus extremos (1
e 15) e seus termos eqüidistantes dos extremos (3
e 13; 5 e 11; 7 e 9), bem como podemos perceber que:
|
|
|
1
+ 15 = 3 +
13 = 5 + 11
= 7 + 9 =
16 .
|
|
| Mas será uma simples coincidência? | |
| Não!! Se generalizarmos para um PA de n termos  ,
onde  , o resultado
se mantém. Confira: |
|
  mmmmmmmmmmmmmmmmmmmmmmmmmmmmm iiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii iiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii |
|
| Aqui, fizemos a álgebra para dois termos da igualde apenas, fica para você fazer o mesmo com os outros e se convencer que a propriedade é válida: | |
|
"Numa Progressão
Aritmética finita,
a soma de dois termos eqüidistantes dos extremos é igual à soma dos termos extremos." |
|
Se fizermos a soma
dos n termos de uma PA finita, teremos  .
Podemos somar esta expressão, de uma forma conveniente, para obter
uma fórmula que nos permita somar n
termos de uma PA finita qualquer, conhecendo o primeiro
e o n-ésimo termos da mesma: |
|
 |
|
|
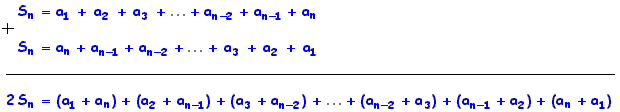Como |
|
  |
|
| de onde surge a conhecida fórmula da soma dos n termos de uma PA finita: | |
 |
e
, 
e 
, ...
e ..., são termos equidistantes dos extremos, suas somas são
iguais a 
;
logo: 