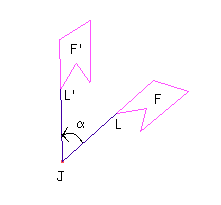
Rotação:Pode ser entendida pela transformação, por giro em torno de J, de um ponto S no plano em um ponto L' de tal forma que os segmentos JS e JL' sejam congruentes.

Uma rotação fica determinada por um sentido (horário ou anti-horário) e por um ângulo de giro.

Veja esta seqüência de rotações: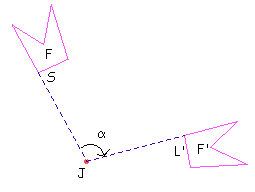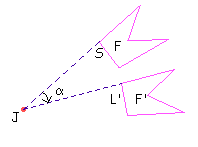







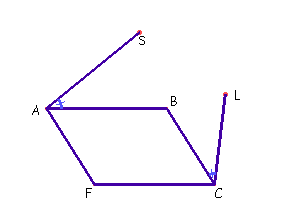
A construção do rotor de Sylvester (instrumento 2) foi feita assim:

Observe a figura.

instr1
  • Construiu-se duas hastes SA e AF de tamanhos quaisquer.
  • Duas outras hastes AB = SA e FC = SA.
  • Duas outras LC = AF e BC = AF.
  • Ângulos SAB = BCL.



Novamente o ponto L faz o papel do lápis da figura a ser rotada a partir de movimento do ponto S.
Para mostrarmos que este instrumento funciona como rotor de figuras basta que mostremos que os ângulos SAB e SFL são iguais e que os segmentos FS e FL sejam também iguais.
Se você quiser ver por que este instrumento realmente rota figuras, clique aqui.
volta à pag. principal