Nosso propósito aqui é estudar uma transformação especial, que quando aplicada a figuras do plano pode alterar suas medidas, ampliando ou reduzindo a figura original, ou seja, é uma transformação que relaciona figuras semelhantes.

O instrumento que apresentamos anteriormente, o pantógrafo ( pantos = tudo + graphein = escrever ) corresponde a esta transformação: amplia ou reduz a figura original.

Vamos entender agora por que o pantógrafo de fato realiza tal transformação.

Para isto precisamos deixar claro os princípios de construção do instrumento:

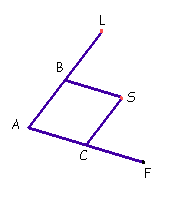
Observe a figura.

• Construiu-se duas hastes AL e CS observando que o fator de ampliação é dado por AL / AB.

• Uma terceira haste FA = AL.

• Outra haste BS = AL - CS.

• Marcou-se em FA um ponto C e em AL um ponto B tais que: AC = BS e AB = CS.

Observe que os pontos L e S, percorrem a figura a ser reproduzida, assumindo os papéis de lápis ou ponta seca de um compasso. A figura é ampliada se escolhermos o ponto S como ponta seca e é reduzida se escolhermos L como ponta seca.

Para que este instrumento realmente funcione como um 'ampliador' de figuras é preciso que AL / AB seja igual a FL / FS, isto é, S deve pertencer à reta FL. Se você estiver interessado em saber a matemática que 'está por trás' disto, clique aqui.