TEOREMA DE PITÁGORAS
Márcia Rodrigues Notare *
Daniela Stevanin Hoffmann *
Maria Alice Gravina *
Curso de Licenciatura em Matemática da UFRGS

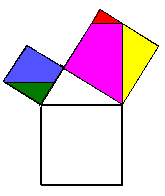
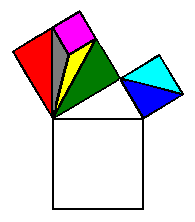
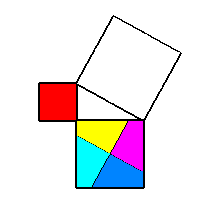O Teorema de Pitágoras diz que,
em um triângulo retângulo,
o quadrado da hipotenusa é igual
à soma dos quadrados dos catetos. 
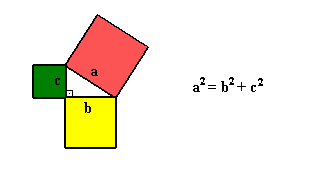
Se construírmos quadrados sobre os lados
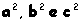a, b e c do triângulo retângulo, esses quadrados terão área .
Assim podemos enunciar o Teorema de Pitágoras da seguinte forma:
a área do quadrado construído sobre a hipotenusa é igual à soma das áreas dos dois quadrados construídos sobre os catetos. 
Podemos tornar o entendimento do Teorema mais lúdico por meio de RECORTES que nos ajudem a visualizar sua demonstração. A partir de critérios de recorte aplicados aos quadrados menores (construídos sobre os catetos), podemos montar o quadrado maior (construído sobre a hipotenusa) através de quebras-cabeça que ilustram,  e até mesmo demonstram, o Teorema de Pitágoras!
A seguir, mostraremos três quebra-cabeças para você brincar: tente montar,
com as peças coloridas, o quadrado maior e procure identificar com que critérios de
recorte foram construídas essas peças a partir dos quadrados menores. Se você quiser,
pode obter ajuda e ver os critérios de recorte e a demonstração que explicam porque
o quebra-cabeça funciona e obter os arquivos Cabri para download.
 
Volta para ATIVIDADES

Márcia Rodrigues Notare é licenciada em Matemática e mestranda em Informática na Educação, Instituto de Informática-UFRGS. E-mail:notare@inf.ufrgs.br
Daniela Stevanin Hoffmann élicencianda em Matemática e bolsista da Prof. Maria Alice Gravina. E-mail: dsh@mat.ufrgs.br
Maria Alice Gravina é professora do curso de Licenciatura em Matemática da UFRGS, mestre em Matemática pelo IMPA-CNPq e aluna do programa de doutorado em Informática na Educação-UFRGS. E-mail:gravina@mat.ufrgs.br