DEMONSTRAÇÃO

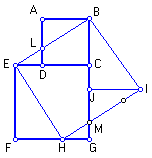
Após dispor um quadrado sobre o outro, traçamos o segmento BE e as retas r e s perpendiculares à EB passando, respectivamente, pelos pontos E e B. Seja H o ponto de r sobre o segmento FG. Traçamos a reta perpendicular à EH passando por H e seja I o ponto de intersecção desta reta com s. Traçamos IJ perpendicular à BG.
Após esta construção temos que BEHI é retângulo. Vamos então, inicialmente, mostrar que de fato é quadrado, para isto mostrando que EB e EH são congruentes.Os triângulos EFH e ECB são congruentes já que ambos retângulos, com catetos EF e EC congruentes (são lados do quadrado ECGF) e ângulos FEH e CEB congruentes (cada um deles somado ao ângulo CEH completa 90 graus).
Sobre a congruência que garantem o encaixe das peças:
*os triângulos FEH e JBC são congruentes pois retângulos e tem os lados EH e BC congruentes (lados opostos de retângulo), os ângulos FEH e JBI congruentes (ângulos com lados paralelos)
*os triângulos LAB e MJI são congruentes pois retângulos com lados AB e JI congruentes (AB e BC congruentes, e BC por sua vez congruente à JI, já que por transitividade são congruentes os triângulos JBI e CEB) e ângulos ABL e JIM congruentes (ângulos com lados paralelos)

*os triângulos HGM e EDL são congruentes pois retângulos com lados EL e HM congruentes (EL=EB-LB , HM=HI-MI , e são congruentes EB e HI, assim como LB e MI) e ângulos DEL e GHM congruentes (ângulos com lados paralelos).

A verificação das congruências nos garantem que os recortes feitos nos quadrados ABCD e ECGF, de fato, permitem montar o quadrado maior BEHI.



Volta para Dois Quadrados Transformados Num Quadrado