DEMONSTRAÇÃO

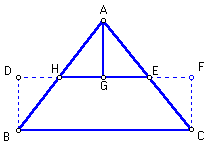
Sobre o triângulo dado ABC, construímos um retângulo com base igual à um dos lados do triângulo e o lado paralelo à base passando pelos pontos médios de AB e AC. Traçamos o segmento AG perpendicular à HE.
Devemos mostrar que os dois triângulos no triângulo dado são congruentes aos triângulos pontilhados do retângulo. De fato isto acontece:  
1.Os triângulos AGH e BDH congruentes pois:
*os lados AH e BH são congruentes já que H é ponto médio de AB
*os ângulos AGH e BDH são retos
*os ângulos AHG e BHD são congruentes já que opostos pelo vértice
2.Com raciocínio análogo mostra-se que também são congruentes os triângulos AGE e CFE.

Assim podemos concluir que as peças que compõe o triângulo ABC se encaixam perfeitamente no retângulo construído.


Volta à Triângulo Transformado em Retângulo