Modellus_tutorial

APRESENTAÇÃO

Criado por Vitor Duarte Teodoro vdt@mail.fct.unl.pt
Colaboração de João Paulo Duque Vieira e Filipe Costa Clérigo
CopyrigthÓFaculdade de Ciências e Tecnologia, Universidade Nova de Lisboa

O Modellus é uma ferramenta de modelagem, simulação e cálculo. Permite que professores e alunos estudem fenômenos físicos, químicos, biológicos, econômicos, entre outros, descritos através de "modelos matemáticos".
Pode ser utilizado tanto no ensino básico como no médio ou até mesmo no superior, pois compreende desde conceitos bastante simples, como a proporcionalidade, até tópicos mais avançados, como a resolução de um sistema de equações diferenciais ordinárias.
Excelente ferramenta para professores, em especial os de matemática, que pretendem trabalhar num contexto interdisciplinar ou que estejam querendo despertar nos alunos o interesse pela ciência.
O Modellus apresenta diversas formas de visualização dos resultados tais como gráficos, animações e tabelas. Aprendendo a lidar com essas ferramentas, professores e alunos terão um importante aliado no processo de ensino-aprendizagem.
A versão 1.11 já conta com diversos exemplos na física, química e matemática, além de uma pasta com diversas imagens que podem ser utilizadas nas animações.
O Modellus permite que estudantes interajam com os fenômenos que estão sendo estudados de forma dinâmica, ao contrário da forma estática que estamos acostumados a lidar em sala de aula.
Para preparar um modelo, é necessário apenas que se digite as equações matemáticas da mesma forma que elas são escritas no caderno (obedecendo certas normas como veremos adiante) e que se selecione a forma de visualização dos resultados.

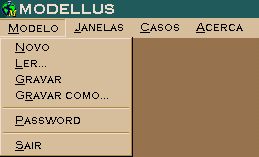
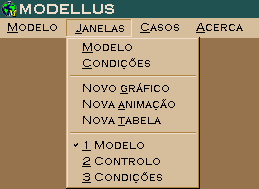
O menu apresenta os seguintes itens: Modelo, Janelas, Casos e Acerca. Cada item, abre para novas ações, conforme especificado abaixo:

Modelo

Novo	Prepara o Modellus para que seja criado um novo modelo
Ler	Abre os diretórios onde se encontram os arquivos, modelos
Gravar	Salva o modelo
Gravar como	Salva o modelo (com nome de no máximo 8 caracteres)
Password	Insere uma senha de segurança no modelo
Sair	Abandona o programa

Janelas

Modelo	Torna visível a janela Modelo
Condições	Torna visível a janela Condições
Novo gráfico	Adiciona um gráfico ao modelo
Nova animação	Adiciona uma animação ao modelo
1 Modelo	Ativa a janela Modelo
2 Controlo	Ativa a janela Controlo
3 Condições	Ativa a janela Condições

Casos

Acrescentar	Acrescenta até 5 casos e condições iniciais ao modelo
Remover último	Remove o último caso da janela Condições

Acerca

Apresenta a versão do Modellus

MODELO

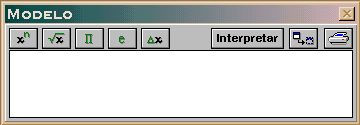
É nesta janela que escrevemos as equações matemáticas de descrevem o fenômeno a ser estudado.
Só é possível ter uma única janela deste tipo.

As equações devem obedecer a seguinte sintaxe:
1. Cada linha deve ter uma única expressão com uma única variável dependente e uma única variável independente. O Modellus considera t, por convenção, como variável independente, mas isto pode ser alterado acionando-se o botão Opção na janela Controlo e nomeando outra variável.
2. As variáveis só podem conter caracteres alfanuméricos, começando por letra, sem espaços nem acentos. Há distinção entre letras maiúsculas e minúsculas.
3. Para escrever potências pressione a tecla ^ ou o primeiro botão da janela Modelo. Se o expoente tiver uma expressão, esta deve ser escrita entre parênteses.
4. Para escrever raiz quadrada pressione a tecla # ou o segundo botão da janela Modelo. Se o radicando tiver uma expressão, ela deve ser escrita entre parênteses.
5. As frações são escritas pressionando-se a tecla /. Se o numerador e/ou o denominador contiverem uma expressão, devemos indica-la entre parênteses.
6. A multiplicação é indicada pela tecla * e deve sempre ser escrita.
7. Os números pi e e são obtidos escrevendo-se "PI" e "e" ou pressionando-se os respectivos botões PI e e da janela Modelo.
8. As funções devem ser escritas de modo explícito, como, y = cos(t), por exemplo.
9. Para calcular a variação de qualquer variável, utiliza-se o botão D da janela Modelo ou pressiona-se a tecla %.
10. Para calcular a derivada de uma função, esta deve ser definida anteriormente.
11. Pode-se calcular derivadas de derivadas, derivando a variável que corresponde à derivada de ordem inferior.
12. Uma equação diferencial deve ser escrita como taxa instantânea de variação igual a uma expressão, variável ou parâmetro.
13. Para escrever comentários na janela Modelo, começar a linha com ;.
14. Para interpretar um modelo, pressiona-se o botão Interpretar, na janela Modelo. A atribuição de valores aos parâmetros e aos valores iniciais só pode ser feita depois do modelo ser interpretado. Se houver algum erro na sintaxe do modelo que foi digitado, o Modellus dará uma mensagem de erro.
15. As variáveis e parâmetros são escritos em itálico na cor verde, os números e operadores em preto e as funções em negrito.
Algumas funções são reconhecidas pelo Modellus, como:

função	descrição	função	descrição
sin( ) ou sen( )	seno	arctan( )	arco tangente
cos( )	co-seno	ln( )	logaritmo natural
tan( )	tangente	log( )	logaritmo decimal
sec( )	secante	rnd( )	número aleatório
arcsin( ) ou arcsen( )	arco seno	abs( )	valor absoluto
arccos( )	arco co-seno	11	11

Da mesma forma, existem algumas instruções reconhecidas:

instrução (exemplo)	descrição
if (t < 10) then (x = 2)	Se a variável t for menor que 10, então a variável x é 2. Note que se não existir outra instrução, a variável x será sempre 2.
if (t > 10) then (a = 0.5)	Se a variável t for maior que 10, a variável a é 0,5.
if (t == 10) then (x = 1)	Se a variável t for igual a 10, a variável x é 1.
If (t <> 10) then (a = 3)	Se a variável t for diferente de 10, a variável a é 3.
if (t >= 10) then (x = 5)	Se a variável t for maior ou igual a 10, a variável x é 5.
if (t <= 10) then (a = 0.5)	Se a variável t for menor ou igual a 10, a variável a é 0,5.
if (t > 10) and (r > 5) then (x = 3)	Se a variável t for maior que 10 e a variável r for maior que 5, a variável x será 3.
if (t > 10) or (r > 5) then (x = 3)	Se a variável t for maior que 10 ou a variável r for maior que 5, a variável x será 3.

CONDIÇÕES

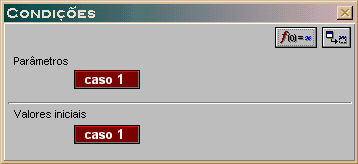Esta janela permite atribuir valores às variáveis e aos parâmetros do modelo, bem como aos valores iniciais das variáveis independentes e das variáveis que estão sendo integradas ou iteradas.

1. Somente depois de acionar o botão Interpretar na janela Modelo é que surge na janela Condições as variáveis e os parâmetros considerados no modelo.
2. Por convenção, o Modellus atribui sempre o valor zero às variáveis e parâmetros. Porém, se houver necessidade, esse valor pode ser alterado, digitando-se o valor desejado na caixa da respectiva variável ou parâmetro.
3. Nesta janela podem ser criados até cinco casos, ou seja, até cinco conjunto de valores.

CONTROLO

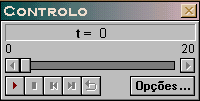
Esta janela permite a interpretação do modelo.
Assemelha-se um painel de videocassete ou de um gravador.
Possui botões para começar, suspender, continuar, parar, voltar ao valor inicial, ir até o valor final e repetir.
É a única janela que fica sempre visível.

1. O botão Opções... permite:
* designar a variável independente, isto é, se você desejar que a variável independente não seja designada por t.
* definir o intervalo que a variável independente pode assumir (limites mínimo e máximo).
* definir o passo da variável independente.
* definir a precisão dos valores apresentados nas várias janelas (casas decimais).
* escolher a forma de exprimir os ângulos (radianos ou graus).
* indicar se o modelo é iterativo, ou seja, um modelo sem nenhuma variável independente explícita.

GRÁFICOS

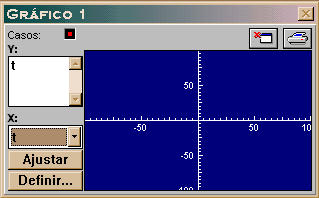Esta janela permite que se construa gráficos em duas dimensões num eixo de coordenadas cartesianas.

1. O eixo vertical é designado por y e o eixo horizontal, por x.
2. Por convenção, o eixo horizontal representa a variável independente t. Mas isto pode ser alterado, clicando-se no botão da barra de rolagem indicativa do eixo x. Note que a variável independente (na janela Controlo) deve ser a mesma variável representada no eixo x. Neste eixo, só pode ser representada uma única variável.
3. O eixo y representa a variável independente. Pode-se representar mais do que uma variável no eixo y, utilizando-se a tecla Shift ou Ctrl em conjunto com o botão esquerdo do mouse.
4. Os gráficos podem ter escala automática (por convenção) ou escalas iguais nos dois eixos. Podem apresentar linhas de chamada e podem ser de pontos.
5. O botão Ajustar permite que você visualize o gráfico em todo o domínio de definição do mesmo, ou seja, dentro dos limites estipulados na janela Controlo.

ANIMAÇÕES

A janela de animações tem botões para criar partículas (objetos) que se movem, imagens que mudam de dimensões, vetores, barras horizontais e/ou verticais, ponteiros que giram, gráficos, valores, colocar textos ou imagens e definir o fundo.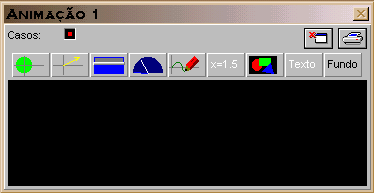

1. Pode-se abrir até três janelas de animações no modelo.
2. Para redimensionar a janela de animações, utiliza-se o botão esquerdo do mouse.
3. Pode-se inserir uma imagem no lugar de uma partícula (objeto), bastando, para isso, selecionar a imagem desejada na lista de imagens disponíveis na versão 1.11.
4. Na animação lápis (gráfico) não se pode representar mais de uma variável em cada eixo.

TABELAS

Esta janela permite acompanhar a um determinado intervalo todo o comportamento do modelo.

1. Pode-se abrir até três tabelas no modelo.
2. Para visualizar várias variáveis utiliza-se a tecla Ctrl ou Shift em conjunto com o botão esquerdo do mouse.
3. Para melhorar a precisão dos resultados, pode-se aumentar o número de casas decimais na janela Controlo botão Opções.