A IMPORTÂNCIA DA ORDEM NOS CASOS DE CONGRUÊNCIA DE TRIÂNGULOS

Eduardo Melloni Lucchesi

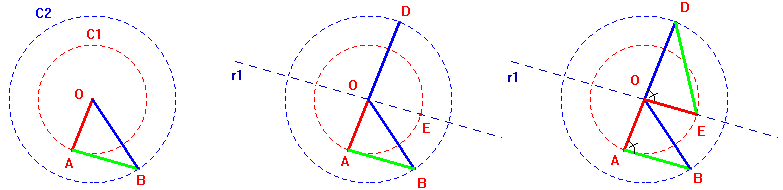
Abaixo são apresentadas construções em que os dois triângulos, com certeza, tem três elementos respectivamente congruentes . Nas animações pode-se identificar mais elementos em congruência e no entanto os triângulos não são congruentes. Descubra situações em que se consegue quatro elementos respectivamente congruentes nos dois triângulos! As animações aqui apresentadas tem como propósito chamar a atenção para a importância da ordem em que são tomados os elementos quando falamos nos casos LAL ou ALA de congruência de triângulos ( ver estes casos ) . Ou seja a notação LAL e ALA guarda importante informação.

Nas construções 1, 2 e 3 são apresentados três casos diferentes em que os dois triângulos apresentam, respectivamente, dois lados e um ângulo em congruência. E no entanto os triângulos não são congruentes. Movimentando os pontos A e B, nas animações, é possível garantir mais elementos em congruência!

CONSTRUÇÃO 1 - ver animação da construção 1

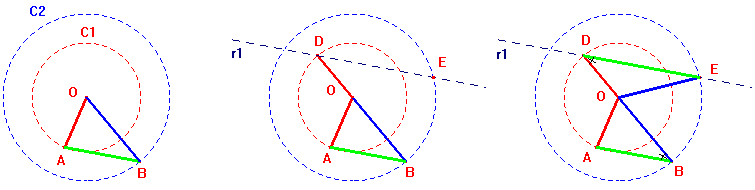
CONSTRUÇÃO 2 - ver animação da construção 2

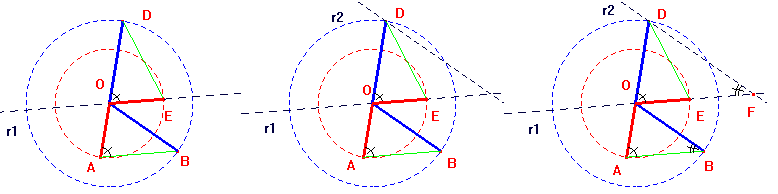
CONSTRUÇÃO 3 - ver animação da construção 3

 

(*) Aluno do curso de Licenciatura em Matemática da UFRGS/IM, orientado pela professora Maria Alice Gravina.

PERGUNTAS:

1. Você saberia dizer, em cada construção, como a reta r1 foi criada?
2. Você saberia dizer, em cada construção, como o segmento OD foi criado?
3. Você seria capaz de criar outras construções de dois lados e um ângulo congruos sem que haja congruência dos triângulos?
4. Você saberia dizer, na construção 3, como surge o ponto F?
5. Quantas soluções você consegue encontrar na terceira construção?
6. É possîvel criar outras construções de dois lados e três ângulos congruos sem que haja congruência dos triângulos?
7. Em que caso, se existe algum, ou, em que casos a ordem dos elementos não importa?

 

 

 

 

 

ELEMENTOS DOS TRIÂNGULOS: LADOS E ÂNGULOS

CASOS DE CONGRUÊNCIA:

1º caso - LAL

Se dois triângulos tem ordenadamente congruêntes dois lados e o ângulo compreendido, então eles são congruêntes.

2º caso - ALA

Se dois triângulos tem ordenadamente congruêntes um lado e os dois ângulos a ele adjacentes, então estes triângulos são congruentes.

3º caso - LLL

Se dois triângulos tem ordenadamente congruêntes os três lados, então estes triângulos são congruentes.

4º caso - ALAo

Se dois triângulos tem ordenadamente congruêntes um lado, um ângulo adjacente e o ângulo oposto a este lado, então estes triângulos são congruentes.
5º caso - reto

Se dois triângulos retângulos tem ordenadamente congruêntes um cateto e a hipotenusa, então estes triângulos são congruêntes.

volta para o topo da página