| (*)
Ricardo Ribeiro
O objetivo desta atividade é
fazermos uma animação da planificação do tetraedro
utilizando o programa Wingeom. No software Poly estas
animações estão prontas e você pode ter uma idéia de
como funcionam.
Para fazer o download dos programas Poly e Wingeom vá em
Software.
Iniciaremos determinando os
vértices da planificação em um sistema de
coordenadas.
Tomando como triângulo central os pontos
A(-1, 0, 0), B(1, 0, 0) e C(0, √3, 0)
teremos, após realizarmos os cálculos, que os
outros pontos serão D(0, -√3, 0), E(2, √3,
0) e F(-2, √3, 0)
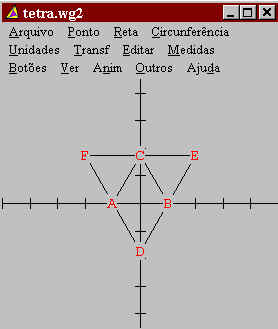
Fixando os
pontos A, B e C, teremos que as faces FAC, ECB e
DAB é que realizarão o movimento da nossa
animação. Precisamos, primeiramente, determinar
o ponto aonde os vértices F,E e D irão se
encontrar. Chamemos esse ponto de G. Perceba que
as coordenadas x e y do ponto G serão a mesma do
centro do triângulo ABC. temos, então, que
descobrir qual o valor da coordenada z.
|
|
|
Seja Q o centro do triângulo ABC, H
ponto médio do segmento AC. Para sabermos quanto
vale a coordenada z precisamos descobrir o valor
do segmento QG.
Como o triângulo AGC é congruente ao triângulo ABC, temos que o valor numérico de HG
é igual a altura do triângulo ABC, e que o
valor de HQ é igual a um terço dessa altura.
Aplicando Pitágoras chegaremos que QG = (√24)/3.
Portanto teremos o ponto G(0, (√3)/3, (√24)/3).
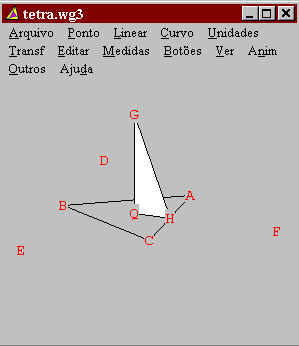
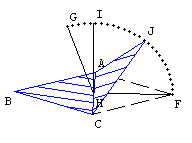
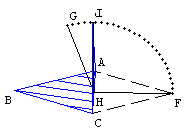
Agora que já determinamos os quatro vértices do nosso tetraedro, precisamos definir como será o movimento das faces.
Vamos olhar para a face ACF, pois o movimento das outras faces saem de modo análogo.
|
|
|
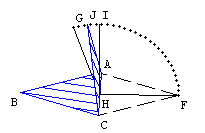
Note que quando a face ACF se movimentar o ponto F irá se deslocar sob um arco de circunferência com centro no ponto H e extremidades nos pontos F e G. Como F está fixo construiremos um ponto J que esteja sob esse arco.
O
programa Wingeom nos permite definir um ponto como a a combinação
linear de três
pontos (2 coordenadas relativas), como queremos que J
esteja sob um arco, precisaremos que esses três pontos formem
um triângulo isóceles e retângulo, para assim utilizarmos o
teorema de Pitrágoras.
Precisaremos então construir um ponto I, de tal forma
que o comprimento de HI seja igual ao comprimento de HF e que
IHF formem um triângulo retângulo.
Note
que o ponto I terá a mesma coordenada x e y que o ponto H, porém a coordenada z será igual ao comprimento de
HG, que por sua vez é igual ao comprimento de HB que é a
altura do triângulo ABC. As coordenadas x e y de H podem ser calculadas facilmente usando trigonometria. Temos então que o ponto será
I(-1/2,
(√3)/2, √3)
Agora vamos determinar J como a combinação linear de HF e
HI, utilizando a opção Ponto/2 coordenadas relativas...
Note que o ponto valerá HF*cos# e HI*sin#.
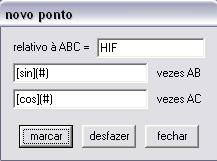
O problema agora é descobrir quanto vale o ângulo GHF, que será o valor máximo que poderá chegar o parâmetro
#.
|
|
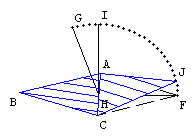
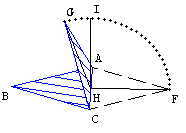
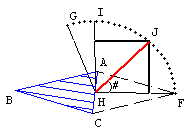
Para descobrirmos o valor do
ângulo GHF vamos analisar a figura ao lado.
Observe que o
valor do ângulo GHF é igual a 180º menos o valor
do ângulo GHQ. Precisamos, então calcular o valor do
ângulo GHQ, que chamaremos de ø. Pelo teorema de Pitágoras, temos que senø será igual ao comprimento de QH dividido pelo comprimento de GH. Logo
aplicando arcoseno temos que ø será
aproximadamente igual a 70,52º
|

|
| |
|
Pronto agora temos que # será maior
que zero e menor que 109,48.
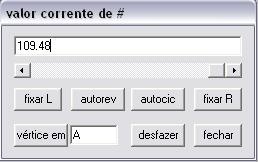
Fazendo raciocínio
análogo encontramos os pontos P e O, que
também irão variar de acordo com o parâmetro
#.
Agora
precisamos plotar esses pontos no programa
Wingeom. Vamos em Ponto/2
coordenada relativas... e colocamos [sin](#)
relativo ao vetor que está na vertical, e
[cos](#) ao vetor que está na horizontal. Agora
vá em Anim/Variação de
# ... e faça # variar
de 0 até 109,48.
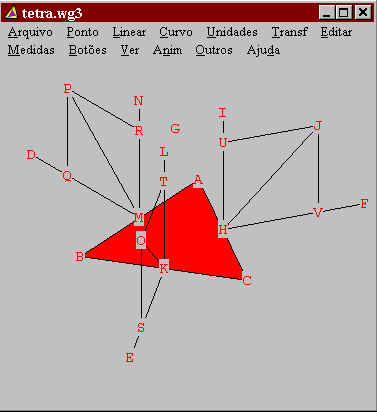
Para terminar
vá em Linear/Segmento
ou face... e crie as faces ABC, ACJ, ABP e
BCO. Para colorir vá em Editar/Elementos
lineares...
Agora já
está pronto sua animação.
|
|
(*)
Aluno do curso de Licenciatura em Matemática da UFRGS/IM,
orientado pela professora Maria Alice Gravina.
|










