2. Circunferência
Dados um ponto O e um número positivo r, a circunferência de centro O e raio r é o conjunto de pontos P do plano tais que a distância de P à O é igual à r .
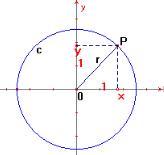
2.1. Equação da circunferência de centro na origem O = (0,0)
|
Na figura 1, tomando o triângulo retângulo formado pelos pares ordenados (0,0), (x,0) e (x,y) e utilizando o teorema de Pitágoras, obtemos a seguinte equação para a circunferência: x ² + y ² = r ² |
figura 1 |
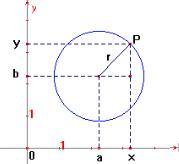
2.2. Equação da circunferência de centro O = (a,b)
|
Este é o caso da figura 2 que representa uma circunferência com centro no ponto (a,b). Aplicando novamente o Teorema de Pitágoras, agora no triângulo retângulo de catetos (x-a) , (y-b) e hipotenusa r, temos a seguinte equação para a circunferência: (x – a) ² + (y – b) ² = r ² |
figura 2 |
2.3. Desigualdades
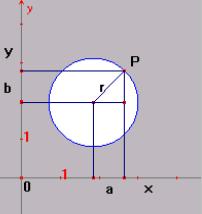
A
relação de desigualdade (x – a)²
+ (y – b)² > r² representa
todos os pontos P = (x , y) que estão no exterior da região
delimitada pela circunferência de centro O = (a, b) e raio r, a região
indicada na figura 3.
Já a relação de desigualdade (x
– a)² + (y – b)² < r² representa todos
os pontos P = (x , y) que estão no interior da região delimitada
pela circunferência, a região indicada na figura 4.
|
figura 3 |
figura 4 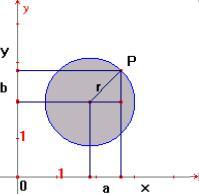
|