1. Retas
1.1. Equação
figura 1 |
figura 2 |
|
 |
 |
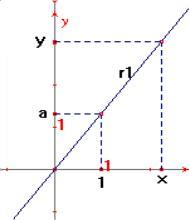
Os triângulos retângulos de catetos medindo, respectivamente 1 e x, são semelhantes (critério: AAA) e assim podemos estabelecer as seguintes relações:
|
Na
figura 1, caso em que a > 0 :
|
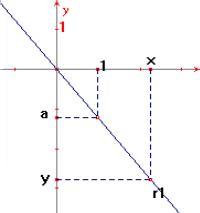
Na
figura 2, caso em que a < 0:
|
Logo
concluímos que a equação da reta que passa pela
origem do plano cartesiano é: |
1.2. Análise da inclinação da reta
Na equação y = a.x o coeficiente a informa sobre o tipo de inclinação da reta em relação ao eixo x. Observe as situações abaixo:
figura 3 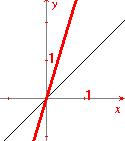 |
figura 4 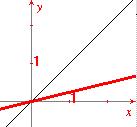 |
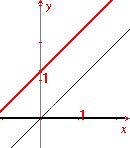
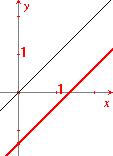
Na figura 3, a reta preta y=x e a reta em vermelho tem equação y=2.x ; já na figura 4, a reta preta tem equação y=x e a reta em vermelho tem equação y=(1/2 ).x Pense:
como se posicionam os gráficos de |
1.3. Análise do deslocamento vertical da reta
Vamos agora determinar a equação de uma reta que não passa pela origem do sistema de coordenadas.
|
figura 5
|
|
figura 6
|
Na
figura 5, a reta preta
tem equação y = x e a reta em vermelho
tem equação y = x + b com b > 0 , e tem-se que todos
os pontos P= (x,y) desta reta estão b unidades acima da outra
reta . Já na figura 6, a reta em vermelho
está b unidades abaixo da reta preta.
Pode ser vista como todos os pontos P = (x,y) que posicionam-se b unidades
abaixo da reta preta.
|
Após esta análise de diferentes posições da reta e correspondentes equações, podemos controlar de imediato a posição que se encontra uma reta dada pela equação y = a.x + b . Por exemplo, para localizar a reta de equação y = 2 x + 3 basta, a partir do gráfico de y = x, e depois o gráfico de y= 2 x (efeito "giro na origem" ) e finalmente o gráfico de y = 2 x +3 (efeito "translação vertical" ).
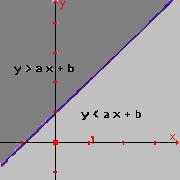
1.4. Desigualdades Todos os pontos P = (x , y) , do plano, que se encontram acima da reta de equação y=ax+b têm as coordenadas satisfazendo a desigualdade y > a x + b e, conseqüentemente, os pontos P= (x , y) que estão abaixo da reta satisfazem a relação y < a x + b |
|
 |