Resolução do Problema 1

Como o nível de água aumenta com o tempo, as funções em questão são do tipo crescente. Isto é, conforme a variável independente "t=tempo" aumenta, a variável dependente "y=altura do nível de água" também aumenta. Os gráficos registram este crescimento, mas mais do que isto, registram o tipo de crescimento. E é isto que queremos entender.

Nos gráficos, os pontos A, B e C representam, respectivamente, a altura do nível de água, num mesmo instante de tempo para os três reservatórios. Vamos imaginar estes pontos em movimento. Com isto podemos ver que:

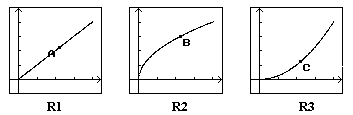• a entrada de água em R1 se processa sempre da mesma forma. Isto é, em intervalos de tempo iguais, a variação do nível de água é sempre a mesma;
• a entrada de água em R2, no início do processo, é mais rápida que no fim. Podemos ver isto ao analisar a variação do nível de água em dois intervalos de tempo iguais: um no início do processo e outro no fim. No intervalo de tempo no início do processo a variação é maior que no intervalo de tempo no final do processo;
• a entrada de água em R3 é lenta no início do processo, e mais rápida no final. Para ver isto repetimos racicínio análogo ao feito no caso do reservatório R2.

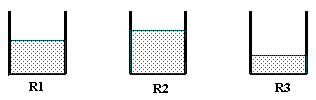
Assim a forma do gráfico nos informa sobre o tipo de crescimento:

• se a curva é do tipo "voltada para baixo", o crescimento é rápido no início do processo e mais lento no fim (caso do reservatório R2);
• se a curva é do tipo "voltada para cima", o crescimento é lento no início do processo e mais rápido no fim (caso do reservatório R3).