CURVAY - CURVAS NO PLANO

A curva mais utilizada no Curvay é a senóide. Vamos relembrar as características dessa curva.

A função Seno:

A curva do seno tal que y=sen(x) tem a seguinte figura:

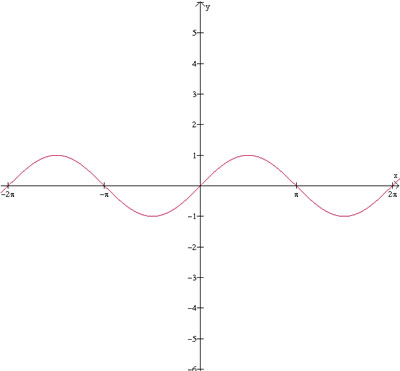
Se deslocarmos a função para a direita, como por exemplo, y=sen(x-2), teremos a seguinte curva:

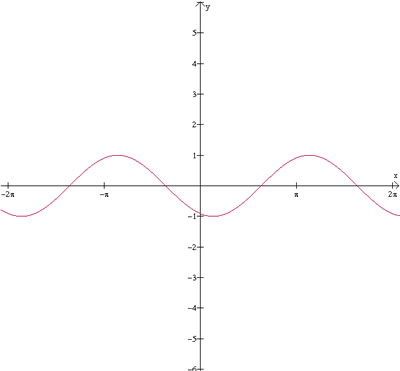
Ao incrementarmos ao x um determinado valor, estamos fazendo um deslocamento horizontal. Portanto, a função tem como lei y=sen(x-k).

Para aumentarmos a altura da curva, precisamos que os valores da imagem sejam ampliados. Usando como exemplo y=2sen(x), obtemos:

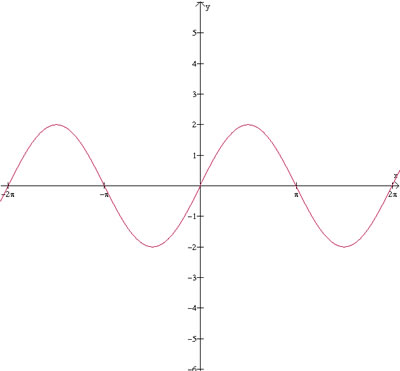
Este valor multiplicando a função nos dá a amplitude da curva, que tem como lei y=c.sen(x). Podemos, também utilizar valores menores que um.

E, em vez de multiplicarmos um valor à função, somarmos um valor, obteremos, usando como exemplo y=2+sen(x):

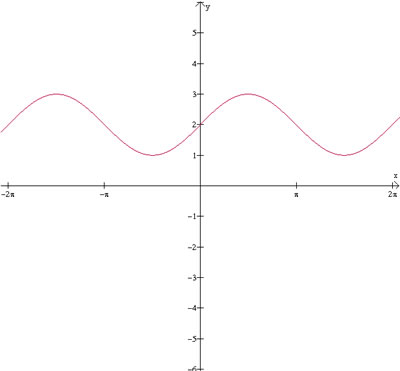
Esta alteração nos dá um deslocamento vertical, que tem como lei y=q+sen(x).

E, finalmente, para que a curva se repita um número diferente de vezes, como em y=sen(2x):

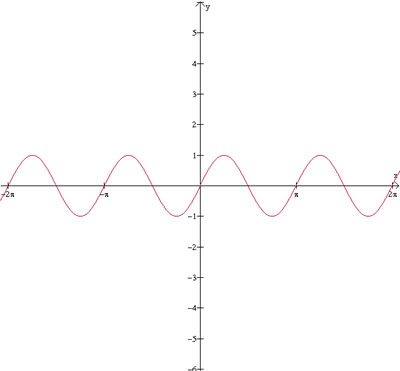
Estamos então modificando a freqüência da curva. Para se obter a freqüência desejada, devemos multiplicar o x pelo inverso do período que queremos obter, o que nos dá y=sen(x/p).

Concluindo, a função seno é uma família de funções do tipo:

y=q+c.sen((x+k)/p)

Onde q, c, k, f são constantes.

Mas, o que aconteceria se a função seno fosse parametrizada, ou seja, se x e y fossem senóides de um parâmetro t?

Veremos.