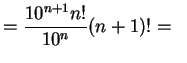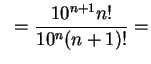| Pág. |
linha |
onde está |
deveria ser |
| Capa |
int.14 |
ln | cossec u + |
ln | cossec u – |
| 2
|
14 |
d x 3
|
d t 3
|
| 2
|
– 14 |
d x / d y
|
d y / d x
|
| 2
|
– 6 |
= (C e x + e 2 x
|
= (C e x + 2 e 2 x
|
| 9
|
– 13 |
– 196 e – t / 20
» 81,1 lb
|
– 196 e – t / 20
|
| 9
|
– 11 |
– 196 e – 0,5
|
– 196 e – 0,5
» 81,1 lb
|
| 38
|
– 15 |
2.37
|
2 × 37
|
| 38
|
– 2 |
é 26,
|
é 2 n,
|
| 42
|
7 |
lim n®
¥ também
|
lim x®
¥ também
|
| 45
|
12 |
1, – 1/2, |
1, 1/2, 2/22,
|
| 46
|
Ex 5 |
n = 2 |
n + 2
|
| 49
|
11 |
n + |
n + 1
*também aumentar
traço da divisão*
|
| 51 |
2 |
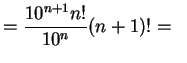 |
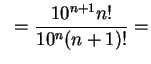 |
| 55
|
9 |
= 0,333
|
= 0,3333
|
| 56
|
5 |
= u2
|
= u1
|
| 57
|
10 |
séries geométricas
importantes
|
séries infinitas importantes
|
| 58 |
8 |
r sn = a + |
r sn = a r + |
| 59
|
3 |
51-l
|
51- k
|
| 59
|
6 |
9/5)1–k
|
9/5) k –1
|
| 59
|
– 6 |
= (– 1/2 + 1/2)
|
= 1 + (– 1/2 + 1/2)
|
| 61
|
Ex 8 |
1/25
|
1/2 k
|
| 61
|
Ex 26b |
4 + x
|
4 – x
|
| 61
|
Ex 26c |
(1 – k) k
|
(– 1) k
|
| 61
|
Ex 29 |
39.
|
29.
|
| 63
|
14 |
(s k – s k ) =
|
(s k –
s k – 1 ) =
|
| 64
|
– 11,
– 4 |
5 5 – 1
|
5 k – 1
|
| 65
|
– 4 |
aproximadamente
|
exatamente
|
| 68
|
Ex 27c |
k = 3 |
k = 2
|
| 69
|
Ex 35a |
< + ln
|
< 1 + ln
*também centrar*
|
| 70
|
– 14 |
c 1 x +
2 c 2 x 2
|
c 1 + 2 c 2 x
|
| 70
|
– 13 |
2 c 2 x 2
|
2 c 2
|
| 71
|
– 11 |
+ 3 · 2c2x + |
+ 3 · 2c3x + |
| 71
|
– 4 |
= 3 · 2c2 = 3!c2 |
= 3 · 2c3 = 3! c3 |
| 72
|
8, 9 |
local de f(0)
|
local de f em x = 0
|
| 72 |
19 |
f ' (0) x2 + |
f ' (0) x + |
| 72
|
– 1 |
função de f (x);
|
função f (x);
|
| 74
|
16 |
f ´´ (x0)
|
f ´´ (0)
|
| 74
|
– 12 |
f (k) (0)
f (k) (0)
|
f (k) (x0)
f (k) (x0)
|
| 74
|
– 7 |
f (k) (0)
|
f (k) (x0)
|
| 74
|
– 4 |
f (k) (x0)
|
f (k) (0)
|
| 76
|
1 |
(2k + 1) |
(2k + 1) !
|
| 76
|
– 1 |
k
|
k !
|
| 77
|
Ex 1c |
p/2 |
p/ 2
|
| 80
|
13 |
S a k
e
S a k
|
S a k
e
S b k
|
| 80
|
17 |
r = 0 ou r =
+ ¥
|
r = 0 ou
r =
+ ¥
|
| 81
|
– 9 |
r = + ¥
|
r =
+ ¥
|
| 81
|
– 1 |
2k |
2k
|
| 82 |
2 |
k + 1k + 1 |
(k + 1)k + 1 |
| 82
|
– 9 |
ou r = + ¥
|
ou r =
+ ¥
|
| 84 |
– 20 |
(2)
O teorema a seguir |
(2)
onde todos os a k são positivos.
O teorema a seguir |
| 89
|
6 |
Assim, (9) é
|
Assim, (8) é
|
| 89
|
– 7 |
3k! |
3k
|
| 90
|
2.6.6.b |
r > 1 or r =
|
r > 1 ou r =
|
| 90
|
2.7.5 |
diverge absolutamente se
|
diverge se
|
| 96 |
7 |
(k + 2)2 |
(k + 1)2 |
| 97
|
Ex 5 |
x3/4 |
x2/4 |
| 97
|
Ex 15 |
k = 0 |
k = 1 |
| 97
|
Ex 20 |
k = 0 |
k = 2
|
| 97
|
Ex 23 |
k = 0 |
k = 1 |
| 98
|
– 3 |
x = x
|
x = x 0
|
| 99
|
13 |
11.9.2 |
2.9.2
|
| 101
|
10 |
que sen 3° =
|
que 3° =
|
| 101
|
19 |
10 – 5
|
10 – 6
|
| 105
|
5 |
+
|
x k +
*no final*
|
| 105 |
12 |
m é um inteiro não-
|
m não é um inteiro não-
|
| 111
|
– 15 |
1 / 1 – x2 =
|
1 / 1 + x2 =
|
| 113
|
– 3 |
x3/3 – x5/5(2!)
|
x3/3 + x5/5(2!)
|
| 114
|
9 |
1/9×4
» 0,747
|
1/9×4! –
1/11×5!
» 0,7467
|
| 123 |
– 16 |
3m (1), |
em (1), |
| 125 |
Figura 3.1.9 |
*O segundo Pi é 2 Pi* |
| 125 |
– 5 |
3.11.1 para |
3.1.1 para |
| 138 |
– 13 |
q = q =
q = q = |
q =
q =
q =
q =
|
| 138 |
– 12 |
q =
£ q |
q =
£ q
|
| 144 |
5 |
(1 – cos q )2 dq = |
(1/2) (1 – cos q )2 dq = |
| 145 |
7 |
o cardióide |
a cardióide |
| 145 |
17 |
12.3.6d e 12.3.6e: |
3.3.6d e 3.3.6e: |
| 145 |
18 e 19 |
*o intervalo de integração das
quatro integrais simples é de
menos a
mais pi terços e não de menos a menos pi terços* |
| 187 |
Ex 35 |
(1 + x
2) no |
(1 + y
2) no
|
| 187 |
Ex 36 |
y = y / (1 + x4) no |
z = y / (1 + y4) no |
| 190 |
18 |
u 1 + w 1 , |
v 1 + w 1 , |
| 190 |
19 |
u 1 + w 1 ,
v 2 + w 2 , |
u 1 – w 1 ,
v 2 – w 2 ,
|
| 193 |
9 |
+ v2 + v 2 + |
+ v22
+ v22 +
|
| 199 |
– 14 |
+ v33 = ||v||2. |
+ v32 = ||v||2. |
| 202 |
4 |
4 j – 4 k |
4 j + 4 k
|
| 209 |
– 12 |
= 0 |
= 0
|
| 209 |
– 9 |
= 0 |
= 0
|
| 211 |
– 10 |
(u × v) |
(u × v) 2
|
| 215 |
Ex 5 |
<0, 1, 2>, |
<0, 1, – 2>, |
| 216 |
Ex 25(b) |
por u e v. |
por u e w. |
| 221 | Ex 17 |
2 = 6 + 2 t |
z = 6 + 2 t
|
| 225 |
– 19 |
v = <8, 5, 1> é |
v = <8, 5, – 1> é |
| 227 |
2 |
+ (y 0
– y 1) + (z 0 |
+ b (y 0 – y 1) + c (z 0
|
| 231 |
– 3 |
ao plano x y têm |
ao plano x z têm |
| 233 |
CONE |
nos planos y z e x y são |
nos planos y z e x z são |
| 233 |
4.7.1 |
texto no Hiperbolóide de
duas folhas:
... paralelos a eles que interceptam a superfície
em mais de um ponto, os traços são hipérboles. |
... paralelos a eles, os traços são hipérboles.
|
| 238 |
6, 12 e 15 |
z = – (x2 – y2) |
z = – (x2 + y2) |
| 239 |
4.7.1 |
(e) 4 z 2 = |
(e) 4 z =
|
| 243 |
– 13 |
r =
r
cos f (1) |
z =
r
cos f (1) |
| 245 |
7 |
r
= cossec f
cossec 2 f |
r = cos f cossec 2 f
|
| 252 |
– 19 |
(– 1, 0, 0) |
(1, 0, 0)
|
| 257 |
Ex 42 |
Seção 4.4 |
Seção 3.4
|
| 262 |
– 7 |
+ t [ – sen t0) i + |
+ t [( – sen t0) i + |
| 262 |
– 4 |
x = cos t0 – sen t0 , |
x = cos t0 – t sen t0 , |
| 316 |
10 |
f (x, y) = x2 – y2 |
f (x, y) = y2 – x2 |
| 316 | 11 |
x2 – y2 = k |
y2 – x2 = k |
| 317 |
3/td>
| interceptos x ... interceptos y ... |
interceptos x iguais a ... interceptos y iguais a ... |
| 321 |
Ex 45 |
f (x, y, z) = |
f (x, y) =
|
| 337 |
10 |
u (x, y) |
u (x, t)
|
| 344 |
– 21 |
(2 x sen y) |
(2 y sen y) |
| 344 |
– 17 |
= 2 ex y cos y |
= 2 y ex y cos y |
| 345 |
21 |
f x = 3 x3 y4 e |
f x = 3 x2 y4 e |
| 356 |
21 |
e f x (x, y) = |
e f y (x, y) = |
| 357 |
Ex 7 |
z = x 2 + |
x 2 +
|
| 357 |
Ex 8 |
z = x 2 y – |
x 2 y –
|
| 358 |
Ex 41 |
calculado de a . |
calculado de q .
|
| 370 |
– 7 |
+ 16(y – 1) + |
+ 16(y – 2) + |
| 372 |
17 |
Delta z / z | |
| Delta z / z | |
| 375 |
4 |
se dz / dz e |
se dz / dx e |
| 375 |
Ex 2 |
4 z 3 ; |
4 z) 3 ; |
| 376 |
Ex 27 |
P(3, 5, 1) |
P(4, 6, 1) |
| 377 |
Ex 63 |
z |
w *o primeiro entre ( )*
|
| 379 |
– 6 |
absoluto |
relativo
|
| 380 |
Fig. 6.8.4 |
* O parabolóide hiperbólico está impresso duplicado * |
| 387 |
Ex 45 |
xi2 ) b = |
xi ) b =
|
| 390 |
– 1 |
de restrição. Como o |
de restrição. |
| 394 |
9 |
que (2, 2, 4) é o ponto |
que (2, 4, 4) é o ponto |
| 403 |
13 |
(1 + 8xy) dxdy = |
(1 + 8xy) dydx = |
| 404 |
– 2 |
dxdy ou |
dydx ou
|
| 405 |
1 |
dydy = |
dydx =
|
| 405 |
2 |
[1/3 xdx = |
1/3 xdx =
|
| 405 |
4 |
b, 0 |
b, c |
| 418 |
– 3 |
[(1 + cos q )2 sen q |
2 [(1 + cos q )2 sen q |
| 421 |
Ex 29 |
4 – y |
4 – y2
|
| 435
|
– 1 |
]3 |
]2
|
| 436 |
– 3 |
+ x 2£ |
+ z 2£
|
| 440 |
23.(a) |
y + 1 |
1 – x
|
| 446 |
8 |
= 1/área de R = *integral dupla* |
= 1/área de R *integral dupla* |
| 449 |
6 |
é 2 p b 2, |
é p b 2, |
| 452 |
7.7.2 |
*trocar os textos de lugar na figura*
|
| 454 |
11 |
y, z) = |
y, z) dV =
|
| 455 |
3 |
13.8.2c , |
4.8.2c , |
| 458 |
5 |
r = r 1 e r
r = 2. |
r = r 1 e r
= r 2.
|
| 479 |
– 9 |
F(r) = – |
F(r) =
|
| 485 |
Ex 12a |
+ 3x 3 – |
+ 3x 2 –
|
| 496 |
– 1 |
x = t , x = t2 |
x = t , y = t2 |
| 499 |
Ex 35 |
+ xzj + |
+ yzj +
|
| 501 |
4 |
(y i + j) |
(y i + x j) |
| 504 |
7 |
y = t |
y = y
|
| 505 |
4 |
f / y |
f / x
|
| 508 |
Ex 8a |
y sen dx – |
y sen x dx –
|
| A12 |
2.4.35 |
n = > |
n >
|
| A13 |
2.7.37 |
39,999 |
39.999
|
| A14 |
2.10.5 |
x 6 + p 6
|
x 6 – p 6
|
|
| A14 |
2.10.25 |
(b) f (5) (0) = 5 |
(b) f (5) (0) = 5 ! |
| A14 |
3.1.5 |
(d) ... (d) ... (d) |
(d) ... (e) ... (f) |
| A16 |
3.3.3 |
(a) ... (b) ... (b) |
(a) ... (b) ... (c) |
| A18 |
Supl 3 |
nada nada nada |
Limaçon nenhum nenhum |
| A20 |
|
Exercícios 4.1 |
Exercícios 4.2
|
| A20 |
4.2.37 |
de raio em torno |
de raio 1 em torno |
| A20 |
|
Exercícios 13.3 |
Exercícios 4.3
|
| A21 |
4.3.21 |
(a) 33/25
(c) -1/5 |
(a) -33/25
(c) 1/5 |
| A21 |
4.3.27 |
49*raiz de*2 para |
49*raiz de*2 N para |
| A21 |
|
Exercícios 13.4 |
Exercícios 4.4
|
| A21 |
|
Exercícios 13.5 |
Exercícios 4.5
|
| A21 |
4.5.19 |
*baixar o sinal para alinhar com o 43*
|
| A21 |
|
Exercícios 13.6 |
Exercícios 4.6
|
| A21 |
4.6.9 |
y + x = 1 |
y + z = 1 |
| A24 |
4.8.31(b), 4.8.33(b) e 4.8.35(b) |
r = |
r = |
| A30 |
6.3.37 |
x / z |
– x / z *deveria caber nesta linha*
|
| A31 |
6.6.53 |
*falta um "(a)"*
|
| A32 |
6.7.55 |
– 2 r sen q
cos 2q |
– 2 r 2 sen q cosq
|
| A32 |
6.7.27 |
363 |
*raiz de* 363 |
| A33 |
6.8.53 |
,709 °C |
,7096 °C
|
| A34 |
7.2.21 |
– 1/2 |
– 7/60
|
| A34 |
7.2.49 |
e 18 |
e 8
|
| A35 |
7.3.31 |
(4/3) a3 |
p a2 h |
| A35 |
7.5.3 |
7 |
47/3
|
| A37 |
8.1.45 |
*falta:*
dy / dx = 1/x,
y = c + ln x
|