
OPERAÇÕES COM NÚMEROS DECIMAIS EXATOS
Os números decimais exatos correspondem a frações
decimais.
Por exemplo, o número 1,27 corresponde à fração127/100.
![]()
onde 1 representa a parte inteira e 27 representa a parte decimal. Esta notação subentende que a fração 127/100 pode ser decomposta na seguinte forma:
![]()
Em particular, os inteiros são números decimais:
![]()
Nesta perspectiva, as operações com decimais
exatos reduzem-se a operações com frações
decimais.
Adição de números na forma
decimal finita
Ao adicionar números decimais exatos, estamos
adicionando as frações decimais que os representam. O resultado
é um número decimal exato.
Por exemplo:
![]()
Mas, para adicionar frações, é preciso reduzi-las
a frações equivalentes com mesmo denominador. A soma será
uma fração decimal, que por sua vez pode ser representada
na forma decimal:
![]()
Outro modo de ver:
![]()
Sabemos operar com inteiros, com o algoritmo das colunas.
Escrevemos os números observando, fazendo as colunas coincidirem:
unidades com unidades, dezenas com dezenas , centenas com centenas, etc.
![]()
Ao operar 12 + 3,54, obedecemos à mesma regra, colocando a vírgula
separando a unidade do décimo, fazendo coincidir: décimo
com décimo, centésimo com centésimo, milésimo
com milésimo, etc.
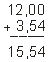
Subtração de números na
forma decimal finita
O mesmo raciocínio pode ser estendido à subtração. O resultado é um número na forma decimal finita.
Multiplicação de números na forma decimal
finita
Analogamente, podemos multiplicar dois números forma decimal transformando
cada um deles em frações decimais e realizar a multiplicação
de numerador por numerador e denominador por denominador. O resultado
é um número forma decimal.
Por exemplo:
![]()
Podemos também multiplicar os números forma decimal como
se fossem inteiros, encontrar o produto, voltar a escrevê-lo como
fração decimal e logo após na forma decimal .
Fazemos isto utilizando o algoritmo da multiplicação de
inteiros.
O algoritmo da multiplicação por inteiros é justificado
com a aplicação das propriedades associativa e comutativa
da adição e a distributiva da multiplicação
com relação à adição:
225×35 = 225 x ( 3.10 + 5) =
(225 x 3 x 10) + (225 x 5) =
(225x5) + (225 x 30) =
1125 + 6570 = 7875
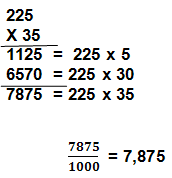
Para evitar esta posterior divisão por 1000, costuma-se contar
e somar o número de casas decimais de cada fator, colocando-se
a vírgula no lugar correspondente: 3 casas implica que a vírgula
vai separar 3 dígitos.
Divisão de números na forma decimal finita
Esta operação é a mais difícil
de justificar, pois ainda não sabemos dividir números inteiros
cujo quociente não é inteiro. Nem sempre o resultado da
divisão de dois números na forma decimal finita resulta
com a mesma forma. Vamos mostrar que pode-se obter como quociente um número
na forma decimal infinita, com período.
|
Caso 1: |
Considerando que os inteiros são números
decimais, sabemos calcular:
36 : 4 = 9
Mas não sabemos, ainda, calcular, em números
decimais, divisões cujo quociente não é inteiro:
36 : 5 = ?
36 : 7 = ?
| Caso 2: |
Neste caso, a divisão pode ser solucionada com auxílio
das frações decimais e da adição com números
decimais.
Exemplos:
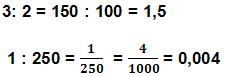
| Caso 3: |
Neste caso, não é possível transformar
a fração resultante da divisão em fração
decimal.
Como fazer?
Exemplo:
7 = 1/7
Adotamos sucessivas multiplicações por 10, buscando expressar
esta fração como uma soma de potências de 1/10, para
ao final obter um número decimal. Salientamos em azul, a primeira
divisão que gera um número inteiro não nulo mais
um resto: 10/7. Salientamos
em amarelo a coleção de restos
que gera uma coleção de divisões.
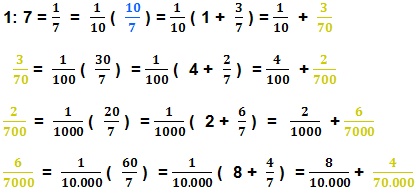
Até este momento, na divisão, obtemos o seguinte:
![]()
Observe que temos uma coleção de restos das divisões:
3, 2, 6, 4...
A pergunta é:
Se continuarmos neste processo, em algum momento o resto vai se repetir,
de tal modo que a coleção de dígitos que forma o
quociente na sua forma decimal, também comece a se repetir?
A resposta é sim: a coleção de restos só pode
percorrer os valores 1,2,3,4,5,6. Não existe resto igual a 7 ou
maior do que 7, quando dividimos por 7.
Vamos completar os cálculos para exemplificar o que queremos dizer:
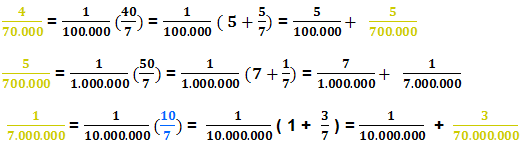
Alguma coisa está acontecendo. Encontramos novamente o quociente
(10/7).
Vamos voltar a procurar o resultado da divisão como soma de potências
de 1/10:
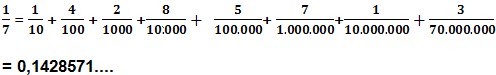
O primeiro dígito ( 1) corresponde à primeira divisão
(10/7) e o último que foi computado, também corresponde
à divisão (10/7).
Quais são os dígitos que seguem o último, completando
os pontinhos?
A coleção de dígitos que forma o quociente, se repetirá:
0,1428571428571428571....
Forma-se um período de 6 dígitos: 142857.
Os restos também se repetem: 3, 2, 6, 4,5,1.
Observe que obtivemos 6 valores diferentes para o resto, de 1 a 6. Impossível
encontrar mais do que isto, pois o divisor é 7.
Algoritmo da divisão
A técnica de divisão aplicada acima justifica o conhecido
“algoritmo da chave”:

Esta técnica pode ser estendida para quaisquer outros pares de números, inteiros ou decimais.Veja animação:Transformação de fração em decimal (AP)
Exemplo:
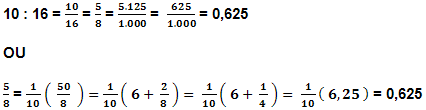
| Caso 4: |
Se os números estiverem em forma decimal, estendemos
a definição de fração para estes números
e transformamos a fração resultante numa fração
equivalente com inteiros.
Exemplos:
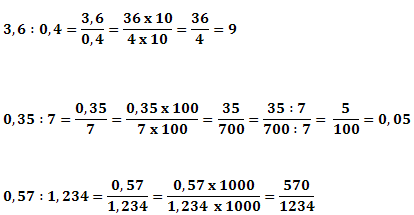
Como visto anteriormente, se multiplicarmos tanto o dividendo como o divisor pelo mesmo número ( no caso, por 10, 100 ou 1000) o quociente não se alterará. Utilizando essas informações poderemos efetuar divisões como se fossem com números inteiros.
Relação de ordem
A comparação de números decimais pode ser feita analisando-se as partes inteiras e decimais desses números.
| Caso 1: |
O maior número é aquele que tem a parte
inteira maior.
Exemplos:
(a) 4,1 > 2,76, pois 4 é maior do que
2.
(b) 3,7 < 5,4, pois 3 é menor do que 5.
| Caso 2: |
Igualamos o número de casas decimais acrescentando
zeros tantos quantos forem necessários. Após esta operação,
teremos dois números com a mesma parte inteira, mas com partes
decimais diferentes. Basta comparar estas partes decimais para constatar
qual é o maior deles.
Exemplos:
(a) 12,4 > 12,31
pois 12,4=12,40 e 40 > 31.
(b) 8,032 < 8,47 pois 8,47=8,470 e 032 < 470.
(c) 4,3 = 4,3 pois 4=4 e 3=3.
BIBLIOGRAFIA
Ensino Fundamental: Frações e Números Decimais. Disponível
em:
http://pessoal.sercomtel.com.br/matematica/fundam/fracoes/fracdec.htm