
Dízimas periódicas... e a Calculadora
José Roosevelt Dias¹
Niterói, RJ
Na RPM 10, p. 23, no artigo "Voltando
a falar sobre dízimas", de Elon Lages Lima, encontram-se resultados
que permitem calcular o número de algarismos do período
de uma dízima periódica simples. O artigo nos conta, por
exemplo, que 1/23 é uma dízima cujo período tem 22
algarismos.
A RPM recebeu, recentemente, um artigo do colega José
Roosevelt Dias, ensinando como uma calculadora simples nos permite obter,
rapidamente, esses 22 algarismos e, em geral, os primeiros algarismos
(20, 30, 40, ..., quantos quisermos) da expansão decimal de 1/n,
n inteiro, diferente de zero.
Extraímos do artigo as principais idéias.
As calculadoras simples têm um visor para 8 dígitos, o que
permitirá obter, cada vez que usarmos a calculadora, 7 dígitos
da expansão decimal de 1/n.
Há um só pré-requisito: é necessário
saber calcular os restos da divisão de ![]() pelo número n. (Através de "congruência"
isto fica fácil ( veja RPM 10, p. 40.)
pelo número n. (Através de "congruência"
isto fica fácil ( veja RPM 10, p. 40.)
Ilustraremos o processo, calculando o período da dízima
periódica 1/23:
1) A calculadora nos diz que 1/23 = 0,0434782 e temos aí os 7 primeiros
algarismos da expansão decimal de 1/23;
![]() = 0,6086956.
= 0,6086956.
Estes são os 7 algarismos seguintes da expansão de 1/23:
1/23 = 0,0434782 6086956;
![]() 0,5217391.
0,5217391.
Estes são mais 7 algarismos da expansão de 1/23:
1/23 = 0,0434782 6086956 5217391;
Está faltando apenas um dígito, por isso vamos continuar:
![]() (Observe o período reaparecendo.) Estes são mais 7 algarismos
da expansão de 1/23:
(Observe o período reaparecendo.) Estes são mais 7 algarismos
da expansão de 1/23:
1/23 = 0,0434782 6086956 5217391 3043478, isto é,
1/23 = 0,0434782608695652173913
O prof. José Roosevelt Dias inspirou-se nas dízimas periódicas
simples para as quais podemos calcular o número de algarismos do
período, mas o processo por ele descrito estende-se para qualquer
fração 1/n, n inteiro, diferente de zero e baseia-se, exclusivamente,
no algoritmo da divisão. O exemplo usado pelo colega foi
![]()
Justificativa
Usaremos o próprio exemplo para justificar o processo:
![]() (1)
(1)
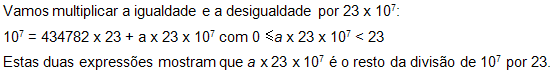
Este resto foi calculado: é 14.
![]()
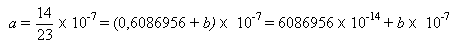
Substituindo em (1):
![]() (2)
(2)
Após multiplicar a igualdade e a desigualdade por 23 x ![]() repetimos o argumento acima:
repetimos o argumento acima:
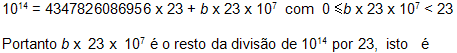
![]()
![]()
Substituindo em (2):
![]()
e assim por diante.
____________________________________________________________________
Notas Finais
¹José
Roosevelt Dias é mestre em Matemática pela Universidade
Federal Fluminense e
professor do Departamento de Geometria desta Universidade.
____________________________________________________________________