O NÚMERO
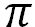
O número 
representa a razão entre a circunferência de um círculo
e seu diâmetro.
No Oriente antigo tomava-se freqüentemente o número 3 como
valor de .
Já no papiro de Rhind, datado de cerca de 1650 a.C., encontrado
no Egito, encontra-se
A primeira tentativa científica de calcular
parece ter sido a de Arquimedes em 240a.C. Esta tentativa foi tão
notável que só se criaram métodos novos para o cálculo
de
em 150d.C. Por isso, analisaremos, aqui, com mais cuidado o método
de Arquimedes, conhecido como método clássico de cálculo
de .
Para facilitar os cálculos, suponhamos que se tome um círculo
de diâmetro unitário. Então o comprimento da circunferência
situa-se entre o perímetro de qualquer polígono regular
inscrito e a de qualquer polígono regular circunscrito. Uma vez
que é uma questão simples calcular os perímetros
dos hexágonos regulares inscritos e circunscritos, facilmente se
obtêm limites para .
Há fórmulas que nos dizem, a partir de um par dado de polígonos
regulares – um deles inscrito e o outro circunscrito - como se podem
obter os perímetros dos polígonos regulares inscrito e circunscrito
com o dobro de número de lados. Com esse raciocínio Arquimedes
calculou
até a segunda casa decimal.
Vários outros matemáticos encontraram aproximações
para ,
porém, não é o objetivo deste texto citar todas as
formas de calculá-lo. O fato mais importante, na tentativa de encontrar
qual o valor exato de ,
foi que ninguém encontrou qual é este valor. Isso se deve
ao fato de que o número
é infinito.
Hoje, parece óbvio dizer isso, mas, até 1767, ninguém
havia conseguido provar tal fato. Nesta época, quem demonstrou
que
é irracional foi o matemático francês, radicado na
Alemanha, Johann Heinrich Lambert.
O símbolo
foi usado primeiramente pelos matemáticos ingleses William Oughtred,
Isaac Barrow e David Gregory, por volta de 1600, para designar a circunferência
de um círculo. O primeiro a usar esse símbolo para a razão
entre a circunferência e o diâmetro foi o escritor inglês
William Jones, numa publicação de 1706. Porém, o
símbolo só encontrou aceitação geral depois
que Euler o adotou em 1737.
Atualmente, já são conhecidas mais de 1 milhão e
trezentas mil casas de .
O MÉTODO DE ARQUIMEDES
O método de Arquimedes consiste em encontrar o valor aproximado
de ,
a partir da construção de duas seqüências de
números, sn e Sn.
A primeira, sn , é construída pelo
cálculo do valor dos lados da seqüência de polígonos
inscritos no círculo de raio 1, e a segunda seqüência,
Sn, refere-se ao valor do lado dos polígonos
circunscritos. Os polígonos inscritos se aproximam do círculo,
por dentro, e os polígonos circunscritos se aproximam do círculo
por fora.
No limite, as seqüências dos perímetros destes polígonos
e se aproximam da circunferência, 2.
Calculam-se assim boas aproximações para ,
a menor e a maior.
Para obter estas duas seqüências, Arquimedes iniciou o cálculo
por s6, o lado do hexágono inscrito no círculo
de raio 1.
É fácil ver que s6 = 1, pois o hexágono
determina, no interior do círculo de raio 1, 6 triângulos
eqüiláteros, com ângulos de 60º e dois lados coincidentes
com raios.
Sabendo que s6 = 1, Arquimedes deduziu o valor
de S6, o lado do hexágono circunscrito ao
mesmo círculo, usando semelhança de triângulos.
Sabendo s6 e S6, Arquimedes
obteve duas seqüências de números: a seqüência
de lados dos polígonos inscritos, com lados 6, 12, 24, 48, 96,
etc ; e igualmente, a seqüência de lados dos polígonos
circunscritos, com lados 6, 12, 24, 48, 96, etc.
Utilizando os valores de s96 e S96
, pelo Método de Arquimedes, calculam-se os perímetros p96
e P96 . Estes valores são muito próximos
de 2.
p 96 < 2<
P96
Dividindo a ambos por 2, obtêm-se duas aproximações
de
3,14016 < <
3,14208
Ou seja, pelo Método de Arquimedes, obtêm-se as duas primeiras
casas decimais de .
