O que é uma progressão geométrica de razão 1/10?
Uma Progressão Geométrica é
uma seqüência de números não nulos, onde qualquer
termo (a partir do segundo) é igual ao antecedente multiplicado
por uma constante. Essa constante é denominada razão
da progressão, que indicaremos por q.
Assim a seqüência de números da forma (a, a.q, a.q²,
a.q³,...) representa uma PG.
Exemplo:
Você pode relembrar na Apresentação: demonstrações
por indução , que está incluída
no módulo I, Módulo dos inteiros.
|
A soma dos n termos de uma PG é dada pela expressão, para q > 0:
Se o primeiro termo da PG não é igual a 1, temos:
|
Exemplos:
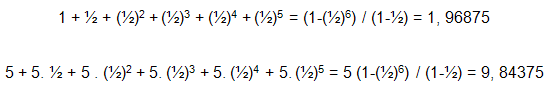
A soma da PG é infinita, quando consideramos todos os termos, isto quer dizer que o número de termos n tende a infinito, é imensamente grande.
Neste caso, se a razão é menor que 1, como
por exemplo, 1/2 ou 1/10, o termo 
da soma se aproxima de zero (faça testes para q = ½ e q
= 1/10, tomando valores grandes para n, tais como 20, 50, etc).
|
Assim, para a soma infinita dos termos
de uma PG
|
Exemplo:
