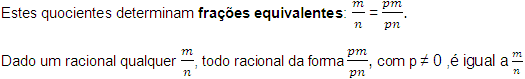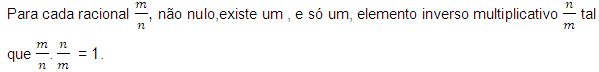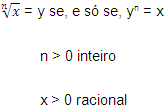CONTRUÇÃO DOS NÚMEROS RACIONAIS, NÚMEROS FRACIONÁRIOS E OPERAÇÕES COM FRAÇÕES
O número racional pode ser definido a partir da aritmética
– fechamento da operação de divisão entre inteiros
– ou partir da geometria - medidas de segementos . Neste texto,
optamos pela abordagem aritmética.
Divisão entre números inteiros
Como já vimos, a operação de divisão é
definida para números inteiros do seguinte modo:
m : n = p se e só se m = n . p, com n |
Nos inteiros, divisão não tem a propriedade
fechamento, pois o quociente m : n é inteiro se e só se
m é múltiplo de n e n ![]() 0.
0.
Múltiplo e divisor de um número:
Para a, b |
Existem propriedades para os números múltiplos
e para a divisão:
Para m, n ![]() Z+
Z+
1. m é múltiplo de 1 e múltiplo dele mesmo, se não
for nulo.
2. 1 é divisor de todos os números inteiros.
3. 0 não divide número algum
4. 0 é múltiplo de todos os números não nulos.
5. Para cada divisão m : n , com n ![]() 0, existe uma família infinita de divisões que têm
o mesmo quociente. Estas divisões são equivalentes e são
obtidas combinando pares de múltiplos e pares de divisores de m
e n, isto é, dados m, n
0, existe uma família infinita de divisões que têm
o mesmo quociente. Estas divisões são equivalentes e são
obtidas combinando pares de múltiplos e pares de divisores de m
e n, isto é, dados m, n ![]() 0 e
0 e
p ![]() 0 , m : n = pm
: pn
0 , m : n = pm
: pn
6. Para cada m, n ![]() 0, m : n = 0 se e só se m = 0.
0, m : n = 0 se e só se m = 0.
É essencial que você estude as demonstrações
destas propriedades, em Apresentação:
múltiplos e divisores.
Fração, número fracionário, reprentação
fracionária
Para completar a operação de divisão, define-se um
novo conjunto numérico, o conjunto dos racionais: Q+
Para isto, amplia-se o conjunto dos inteiros, incluindo todo os quocientes
m : n de números inteiros, desde que
n ![]() 0.
0.
|
|
O conjunto dos números racionais inclui todos
os números resultantes da divisão de inteiros. Por enquanto
estamos restritos aos números positivos, mas todos estes resultados
podem ser estendidos para números negativos. Portanto,![]()
|
![]()
O número racional admite diferentes formas de representação:
representação fracionária (fração ou
número fracionário), representação decimal
(número decimal) ou representação porcentual ( número
porcentual ).
Definições e Operações com frações
![]()
Isto é, conjunto dos inteiros está contido no conjunto dos
racionais.
Exemplos de números racionais fracionários:

|

Número primo
Um inteiro p, não nulo, é um
número primo se admite dois e apenas dois divisores: 1
e ele mesmo p. |
Exemplos: 2; 3; 5; 23.
O número 1 não é considerado primo, pois só
tem um divisor, ele mesmo.
Primos entre si
Dois inteiros p e q, diferentes, são números primos entre si se o único divisor comum entre eles é 1. |
Exemplos de números primos entre si estão nas frações
irredutíveis acima:
1 e 2; 1 e 5; 9 e 16; 9 e 25
A seguir, definimos as operações com racionais :
As justificativas das operações
encontram-se na Apresentação:
definições e justificativas das operações
com racionais. É essencial que você estude este material.
Nas definições, m, n, p, q e outras simbologias dizem respeito
a números inteiros. Sempre que os símbolos estiverem representando
denominadores das frações, está implícito
que é um número não nulo.
Quando quisermos representar um racional com uma única letra, isto
ficará claro.
|
Subtração
Definição
|
Relação de Equivalência

|
![]()
Relação de Ordem

|
![]()
Multiplicação
Definição
|
Divisão

|
Propriedades das operações
Todas as propriedades das operações com inteiros são
válidas neste novo conjunto numérico:
|
a) Leis comutativas e associativas da adição
e da multiplicação; |
Neste conjunto, existe uma nova propriedade:
|
d) Propriedade do Elemento Inverso da Multiplicação
|

e) Lei do Cancelamento para Adição f) Lei do Cancelamento para Multiplicação Se xy = xz então y = z |
A seguir tratamos da potenciação.
Todas as propriedades apresentadas neste
texto são justificadas, na Apresentação:
definições e propriedades das potências. É
essencial que você estude o material desta apresentação.
Potenciação
Neste módulo, vamos restringir-nos às definições
de potenciação com expoente inteiro, positivo, e base fracionária.
Este assunto vai ser plenamente desenvolvido quando tratarmos do conjunto
dos reais completo, incluindo reais negativos.
Definição
![]()

|
Propriedades da Potenciação
Considerando a base como um racional não nulo
e o expoente como um inteiro positivo
1ª propriedade: Uma multiplicação de potências
de mesma base pode ser transformada em uma só potência.
Conservamos a base e somamos os expoentes.
2ª propriedade: Um quociente de potências de mesma base pode
ser transformado em uma só potência.
Conservamos a base e subtraímos os expoentes.
3ª propriedade: Um produto elevado a um expoente pode ser transformado
num produto de potências, com o mesmo expoente.
Conservamos o expoente, multiplicamos duas potências com
o mesmo expoentes.
4ª propriedade: Uma potência elevada a outra potência
pode ser transformada em uma única potência.
Conservamos a base e multiplicamos os expoentes.
5ª propriedade: Base fracionária a = p/q, q ![]() 0.
0.
Em uma fração elevada a um expoente, podemos elevar cada
número a esse expoente.
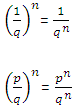 |
Estudando as opções para inclusão do zero
 |
Radiciação
Define-se raiz n de x, para x racional positivo,
como operação inversa da potência. |
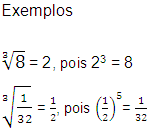
6ª propriedade: Expoente fracionário
Quando definirmos número real, veremos que um número real
positivo qualquer, elevado a um expoente fracionário, corresponde
a uma raiz.
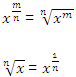 |
Exemplos:
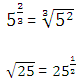
Como conseqüência desta propriedade, temos:
A potenciação é operação fechada
nos inteiros positivos, pois decorre da multiplicação, mas
quando extendida aos números racionais deixa de ser.
Mas radiciação não é fechada nos inteiros
e tampouco nos racionais.
Mostraremos logo mais que raiz quadrada de 2 não é um número
racional. Na verdade qualquer raiz não exata de positivos gera
um número irracional.

Fração
Representações
Potenciação
Radiciação
Este texto foi fundamentado em:
CARAÇA, Bento de Jesus. Conceitos Fundamentais de Matemática.
Lisboa: Gradiva, 1998, páginas 35 a 45, trecho do capítulo
2:1 – A construção do campo racional.