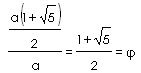O NÚMERO
DE OURO
Prof. Dra. Vera Clotilde Garcia, Acad. Fabiana Fattore
Serres,
Acad. Juliana Zys Magro e Acad. Taís Aline Bruno de Azevedo.
A divisão áurea de um segmento ou a divisão em média e extrema Razão
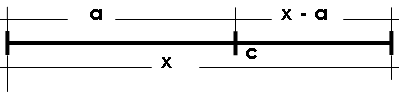
| Dado o segmento AB, dizemos que um ponto C divide este segmento em média e extrema razão se o mais longo dos segmentos é média geométrica entre o menor e o segmento todo: |
|
Ou seja: |
Multiplicando os dois lados da equação por
a (x - a)
obteremos:
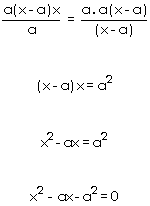
Resolvendo a equação temos:
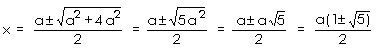
Vamos analisar a raiz positiva da equação por conveniência:
![]()
| O número
é denominado número de ouro. |
Ou seja, a razão entre as medidas dos dois segmentos x e a, é
um número irracional denominado Número de Ouro.
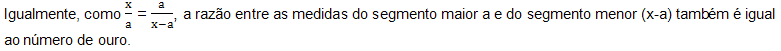
![]()
Propriedades do Número Áureo
Basta considerar o segmento abaixo, no qual x=1, onde c divide o segmento em média e extrema razão,
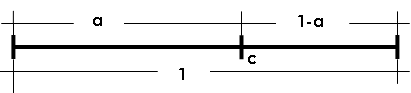
Temos:
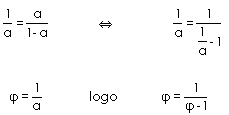
| E conseqüentemente:
E conseqüentemente:
|
O Retângulo Áureo
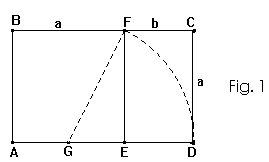
|
Chama-se retângulo áureo, qualquer retângulo ABCD com a seguinte propriedade: se dele suprimirmos um quadrado, como ABFE, o retângulo restante CDEF, será semelhante ao retângulo original. |
Podemos traduzir esta semelhança pela relação:
![]()
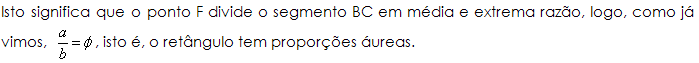
A partir desta relação:
![]()
Vamos verificar que com a operação de “suprimir quadrados”
indefinidamente, sempre encontraremos retângulos semelhantes, mantendo
em cada novo retângulo a razão áurea.
Para isto, a partir da equação 1, multiplicando os dois
lados da equação por (a . b) temos:
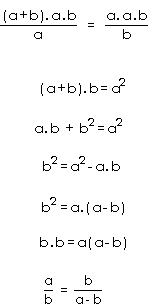
![]()
Notamos que, se pegarmos o retângulo menor da figura 1 :
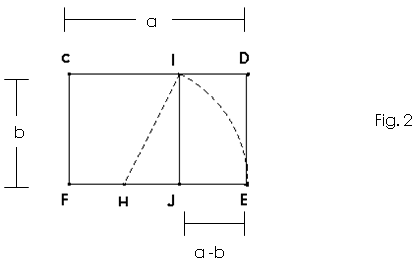
E dele suprimirmos um quadrado, como CIFJ, o retângulo
restante será semelhante ao retângulo CDEF.
Vemos então que a semelhança se mantém:
![]()
ou seja:
![]()
A CONSTRUÇÃO DE UM RETÂNGULO ÁUREO
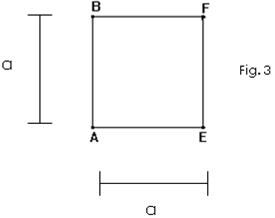
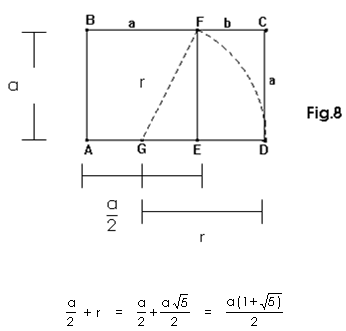
Podemos construir um retângulo áureo partindo de um segmento
AE = a e a partir deste, construir o quadrado ABEF,
como abaixo:
Marcar o ponto médio do segmento AE
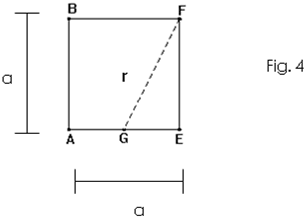
Com a ponta seca do compasso em G e abertura = GF traçar o arco FD, que jaz na reta AE e E é interno ao segmento AD.
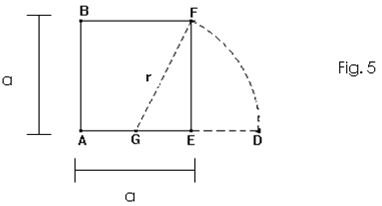
Prolongar o segmento BF e traçar CD perpendicular ao segmento AD.
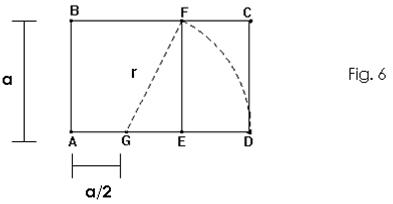
Vemos na figura 6 que : GF = GD = r
E usando o fato de que o triângulo GEF é retângulo em Ê :
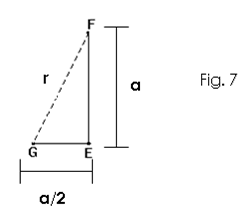
Aplicamos o teorema de Pitágoras e obtemos:
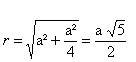
Logo construímos um retângulo de lados:
|
Dividindo o lado maior do retângulo construído pelo menor temos:
Ou seja, o retângulo construído tem proporções áureas. |