Chamaremos de centro de uma região retangular à interseção de suas diagonais. Usando isto provaremos que qualquer reta que contenha o centro de uma região retangular a divide em duas regiões de mesma área.

Demonstração. Se a reta que passa pelo centro da região retangular contém uma das diagonais então ela divide a região retangular em duas regiões triangulares de mesma área. Suponhamos a seguir que a reta não contenha diagonal alguma. Sem perda de generalidade podemos considerar a situação da figura abaixo. M é o centro da região retangular e EF é um segmento que passa por M e divide a região retangular em duas regiões. Vamos verificar que os trapézios ABFE e EFCD e têm áreas iguais.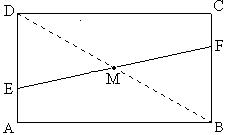

Como AB = CD vemos que as alturas dos trapézios são iguais. Por outro lado, tomando a diagonal BD vemos que D EMD @ D FMB (caso ALA de congruência entre triângulos). Conseqüentemente DE = BF. Tomando a outra diagonal se verifica de modo similar que AE = CF. Portanto, os trapézios têm áreas iguais.

Passamos agora a apresentar a solução do problema dos dois retângulos. Em um plano dado, sejam R1 e R2 e duas regiões retangulares com R2 contido em R1. Seja R = R1 - R2 a região do plano constituída pelos pontos de R1 que não estão em R2.
Consideremos a reta r que passa pelos centros das duas regiões retangulares. Se os centros são diferentes, existe uma única reta r. Se os centros são iguais, tomamos qualquer reta contendo esse ponto. Afirmamos que r divide R em duas regiões de mesma área.
De acordo com o que vimos acima, a reta r divide R1 em duas regiões R1a e R1b de mesma área, e divide R2 em duas regiões R2a R2b de mesma área, onde R1a e R2a estão no mesmo semi-plano em relação à reta. Temos :