Nesta página estão disponibilizados exercícios para serem resolvidos com o apoio de ambientes em geometria dinâmica (Cabri, Sketchpad, entre outros). Para a descoberta de propriedades o dinamismo das figuras se torna importante. Dicas para a resolução dos exercícios estão disponibilizadas, bem como uma página com figuras que podem ser animadas on-line (arquivos java, o que exige um certo tempo para serem carregados).

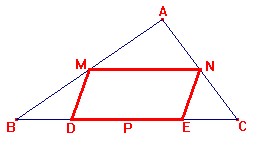
1. Construa um triângulo qualquer ABC e os pontos médios M, N e P de seus lados. Construa os pontos D e P , pontos médios de BP e PC. Construa o quadrilátero MNED. Como deve ser o triângulo ABC para que este quadrilátero tenha alguma regularidade (por exemplo: é quadrado, é retângulo, etc.).
   
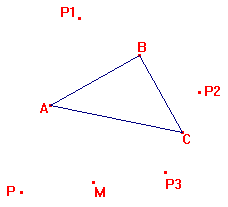
2. Dado o triângulo ABC e o ponto P fora do triângulo, construa P₁ simétrico de P em relação à A; P₂ simétrico de P₁ em relação à B; P₃ simétrico de P₂ em relação à C. Construa o ponto médio M de PP₃. Movimente P e observe o que acontece com M. Justifique o observado.
   
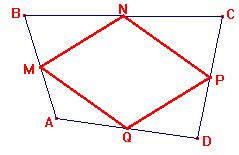
3. Construa o quadrilátero ABCD e os pontos médios de seus lados. Nomeie estes pontos de M, N, P e Q e construa o quadrilátero MNPQ. Movimente os vértices de ABCD e descubra que tipo de figura pode ser MNPQ. Justifique suas descobertas.
   
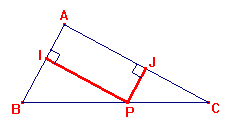
4. Construa um triângulo retângulo ABC, com ângulo reto em A, e P ponto móvel sobre a hipotenusa. Construa os pontos I no cateto BA e J no cateto CA de tal forma que os segmentos PI e PJ sejam perpendiculares aos catetos. Quando o comprimento do segmento IJ atinge seu menor valor? Justifique.
   
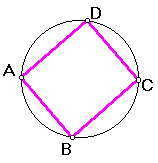
5. Construa um círculo e um retângulo ABC inscrito neste círculo. Movimente os vértices do retângulo e descubra quando o retângulo tem a maior área. Justifique sua resposta.
   
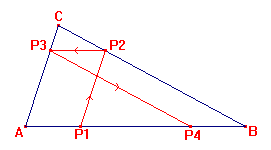
6. Construa um triângulo ABC e prossiga a construção iniciada na figura com o ponto P₁. Observe o que acontece. Justifique o que você está vendo.
   
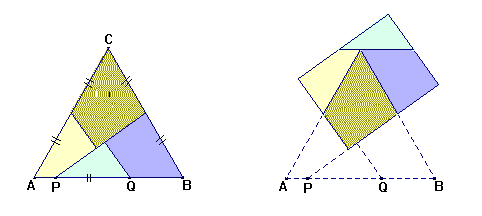
7. Abaixo temos um triângulo equilátero com segmento PQ congruente ao segmento metade do lado do triângulo. De acordo com a construção feita (identificar a construção!), podemos decompor o triângulo de forma a recompor um retângulo de mesma área. Movendo o ponto P mudam-se as dimensões do retângulo em questão. Quem deve ser o ponto P para que o retângulo seja um quadrado? Justificar.
   
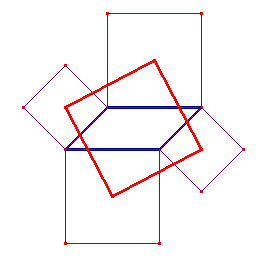
8. Construa um paralelogramo e sobre seus lados construa quadrados. Usando os centros dos quadrados, construa um quadrilátero. Movimente os vértices do paralelogramo e observe regularidades na figura. Enuncie a(s) propriedade(s) observada(s) e demosntre-a(s).
   
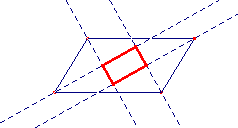
9. Construa um paralelogramo e as retas bissetrizes dos seus ângulos. Construa os pontos de intersecção das bissetrizes e, a partir destes, um quadrilátero. Movimente os vértices do paralelogramo e observe as regularidades da figura. Enuncie e demonstre a propriedade identificada.
   
   
   
   
10. (OMA) Construa um triângulo retângulo ABC com ângulo reto em A. Sobre os lados do triângulo, construa: triângulo ABD com AD=DB e CD//AB; triângulo BCE com BE=EC e EA//BC; triângulo CAF com CF=FA e FB//CA. Que relação existe entre as áreas dos triângulos ABC e DEF.
    
    
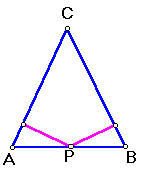
11. Construa um triângulo isósceles e P ponto na base do triângulo. Como é a variação da soma das distâncias de P aos outros dois lados do triângulo? Justifique sua resposta.
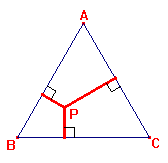
12. Construa um triângulo equilátero ABC e P um ponto em seu interior. Quanto vale a soma das distâncias de P aos lados do triângulo. Justifique sua resposta.