[Exercícios de Exploração]
[Dicas para Resolução] [Figuras em Movimento]
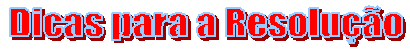
- Procure olhar para alguns triângulos semelhantes (por exemplo, os triângulos ABC e
MNC).
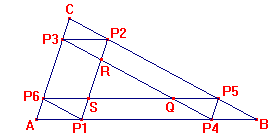
- Considere o quadrilátero PP1P2P3 e os pontos A, B, C e
M como pontos médios de seus lados.
- Olhe para as diagonais do quadrilátero ABCD e procure triângulos semelhantes.
- Olhe para o segmento AP, pois ele é congruente ao segmento IJ.
- Analise a área do triângulo formado pela diagonal do retângulo e dois de seus lados.
A área de tal triângulo mede metade da área do retângulo). Considere a altura deste triângulo
e o raio do círculo.
- Mostre que AP1=AP7, considerando congruências que vêm de
paralelogramos e triângulos.
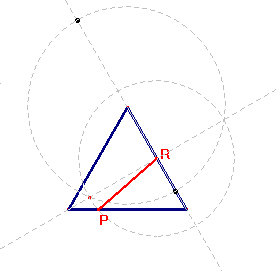
- Mostre que um dos lados do retângulo mede PR, onde R é ponto médio de AC. Assim, este também
será o lado do quadrado na situação particular. Determine o lado do quadrado em termos de
elementos do triângulo. Construa circunferência com raio igual ao lado do
quadrado e centro em R e marque a interseção com o lado AB. O ponto P está construído!
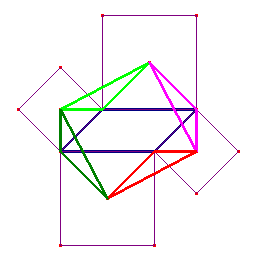
- Analise os triângulos indicados na figura abaixo.
- Mostre que os ângulos internos do quadrilátero serão sempre retos, ou seja, o
quadrilátero será sempre retângulo. Lembre-se que a soma de dois ângulos consecutivos de
um paralelogramo é 180o.
Em que situação este retângulo será um quadrado?
- Observe que a base de DEF é metade da base de ABC (Teorema do Segmento Médio) e que a
altura de DEF é 3/2 da altura de ABC (mesmo motivo). Encontre, então, a relação entre as
áreas destes triângulos.
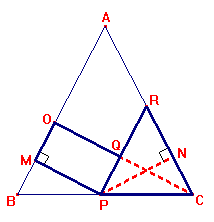
- Trace a altura CO do triângulo relativa ao lado AB. Observe que OMPQ é um retângulo e,
portanto, MP=OQ. Trace uma reta paralela à AB passando por P e nomeie a intersseção de R.
Observe que o triângulo RPC é semelhante ao triângulo ABC e, portanto, é isósceles. Logo,
QC=PN.
- Observe as figuras abaixo: foram construídos três triângulos e aplicados a eles
movimentos de translação. Conclua o resultado.