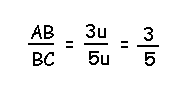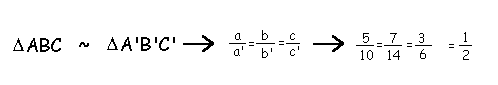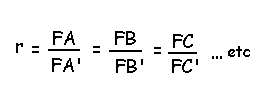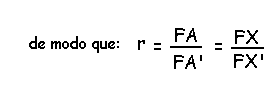|
Quando marcamos um ponto A' sobre a
reta FA, tal que FA' = rFA, chamamos de r, a razão de semelhança.
- Mas o que vem a ser exatamente uma razão de semelhança?
A palavra razão
é usada em matemática quando queremos comparar dois
ou mais elementos.
A razão de um número em relação a outro é
uma comparação entre estes números através de uma divisão. Por exemplo,
se a e b são dois números e b # 0, a razão entre a e b é a/b. Assim
sendo, a razão entre dois segmentos é na verdade a razão entre suas
medidas tomadas na mesma unidade.
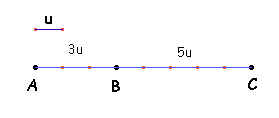
Por exemplo, a razão entre os segmentos abaixo,
AB e BC é 3/5.
 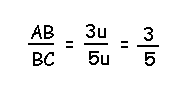
Podemos compreender melhor este conceito,
aplicando-o a figuras geométricas bem simples, triângulos! -Dizemos
que dois triângulos são proporcionais quando as razões dos lados homólogos
(correspondentes) são iguais.
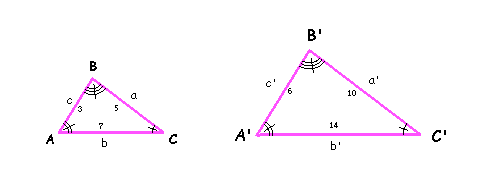
Por exemplo, os lados dos triângulos ABC
e A'B'C' são proporcionais, já que a razão entre seus lados homólogos
(a e a', b e b', c e c') é igual.
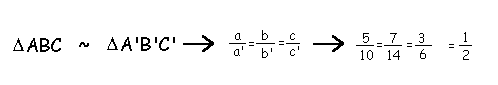
Então quando chamamos de r a razão
de semelhança da figura reproduzida numa homotetia significa que FA'=
rFA, ou seja r = FA' / FA.
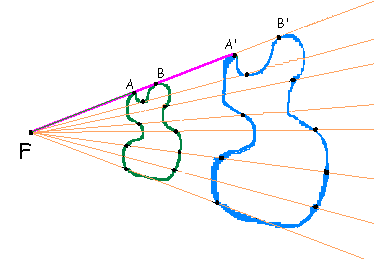
Observe a figura.
Mas o que nos garante que estas figuras
são realmente semelhantes? -Para termos a semelhança assegurada é preciso
que mostremos que a razão entre quaisquer dois segmentos que traçarmos
(a partir de dois pontos em correspondência) nas duas figuras seja igual.
Começamos marcando um ponto X qualquer na figura
1 e seu correspondente X' na figura 2 de forma que os segmentos FX e
FX' tenham a mesma razão de semelhança (r) que FA e FA'. Teremos então
uma figura assim:
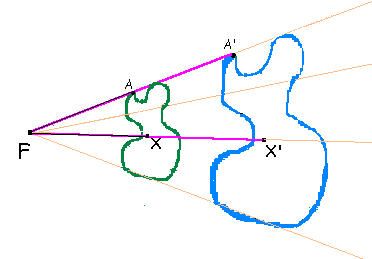
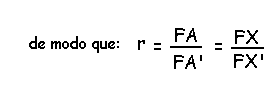
Podemos observar que se ligarmos os pontos A com X e A'com X' teremos
dois triângulos: FAX e FA'X'.
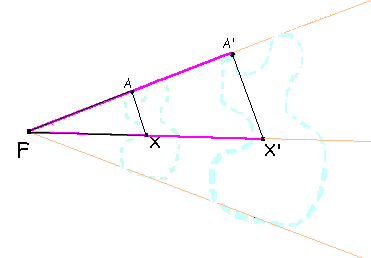
E o que podemos afirmar sobre estes triângulos?
Os lados FA e FA' e os lados FX e FX'
são proporcionais, já que possuem a mesma razão de semelhança (r). O
ângulo F dos dois triângulos é o mesmo. E assim sendo, pelo critério
de semelhança LAL (revisão dos critérios),
podemos afirmar que os triângulos são semelhantes!
Se os dois triângulos são semelhantes, então
os segmentos AX e A'X' são proporcionais aos outros lados dos triângulos.
Então estes lados possuem a mesma razão de semelhança (r) que os outros
pontos da figura. -Agora sim podemos afirmar que estas duas figuras
são semelhantes!
|