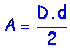LOSANGO
Movimente os pontos vermelhos da figura o observe:
Se quiser montar um retângulo "diferente' rotacione as peças com os pontos pretos.
A Animação Java funciona melhor no navegador Internet Explorer.
Intuitivamente
podemos nos convencer que as peças que compõem o losango se encaixam
perfeitamente na composição do retângulo.
O critério de construção
das peças é:
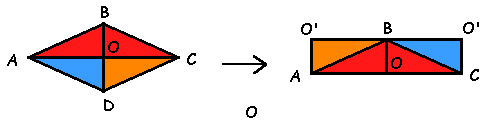
no losango, temos nas diagonais segmentos perpendiculares e que se bissectam (característica de todo e qualquer losango). Essas diagonais dividem o losango em quatro triângulos congruentes que rearranjados formam um retângulo, com a mesma área do losango, conforme indicam as cores.
Sendo nossa abordagem é dentro do espírito da geometria dedutiva devemos mostrar que as regiões triangulares que completam o retângulo obtido a partir do losango são de fato congruentes aos triângulos menores que fazem parte do losango dado.
Veja a demonstração:
Devemos mostrar que os dois triângulos ADO e CDO são congruentes aos triângulos pontilhados do retângulo. De fato isto acontece:
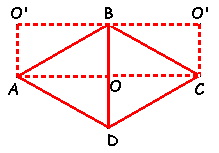
1.Os triângulos ADO e
BCO' são congruentes pois:
*os ângulos OAD e O'BC são congruentes já que são ângulos
entre retas paralelas (AD||BC e AO||BO')
*os lados AD e BC são congruentes já que são lados do losango (que
tem quatro lados congruentes)
*os ângulos ADO e BCO' são congruentes já que são ângulos
entre retas paralelas (AD||BC e DO||CO')
2.Com raciocínio análogo mostra-se que também são congruentes os
triângulos CDO e BAO'.
Assim podemos concluir que as peças
que compõem o losamgo ABCD se encaixam perfeitamente no retângulo construído.