|
|
Daniela Stevanin Hoffmann*
Maria Alice Gravina*
Quando falamos em Áreas de Polígonos, normalmente, lembramos daqueles formulários enormes que são decorados pelos alunos para serem aplicados nas provas e esquecidos logo depois.
Mas por que transformar esse conteúdo em simples "decoreba"?
Essa atividade foi idealizada de modo a fazer
do ensino-aprendizagem das fórmulas das áreas de figuras
planas um trabalho mais lúdico e intuitivo para tentar reverter
essa situação.
A partir da fórmula da área de um retângulo podemos entender
as fórmulas da área de outras figuras planas, utilizando-se a técnica de recortes.
Antes de mais nada, devemos entender que para
determinar a fórmula da área de uma figura precisamos escolher
uma unidade de medida e, então comparar a figura com essa unidade,
isto é, tratamos de responder "quantas" unidades precisamos para
"compor" a figura.
Para deduzir as conhecidas fórmulas
de áreas adotamos como unidade de área um quadrado que,
por definição, tem área igual a 1 u. a. e cujo lado
será tomado como unidade de comprimento (para figuras pequenas,
a unidade usual é um quadrado de lado 1 cm, já para cálculo
de área de um país, por exemplo, usamos um quadrado de área
1 km²).
Vale aqui observar que se mudamos a forma da
unidade de área, por exemplo, se usarmos um triângulo equilátero,
as fórmulas de áreas não serão mais as mesmas.
Mais sobre isso, aqui.
COMO CHEGAR NA FÓRMULA ÁREAretângulo= BASExALTURA ?
O que queremos responder é quantos quadrados unidade "cabem" num retângulo?

Se contarmos a quantidade de quadrados unitários
existentes no interior do retângulo, teremos 15 quadrados, ou melhor,
15 unidades de área.
Agora vamos contar de outra maneira, de tal forma que possamos generalizar
um procedimento para cálculo de área, ou seja, a fórmula.
No exemplo, o retângulo de lados
inteiros m e n
tem m=5 e n=3,
de forma que existem 5 quadrados unitários justapostos na horizontal
em cada linha num total de 3 linhas.
Assim, podemos escrever o total de quadrados
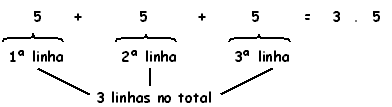
Mais geralmente, se temos um retângulo formado por m quadrados unitários justapostos na horizontal distribuídos em n linhas, contamos o total:
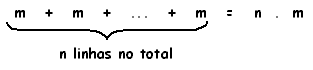
Observe que m
corresponde a medida de um dos lados do retângulo, comumente chamado
de base e n corresponde
a medida de outro lado do retângulo, chamado de altura.
Assim, a fórmula da área do retângulo será
igual a:
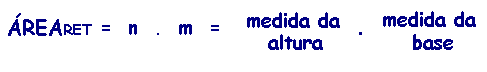
ou simplesmente
ÁREARET = BASE x ALTURA
Para ver isso, clique aqui.
Entendida a fórmula da área de um retângulo, podemos começar a deduzir as fórmulas de área de alguns polígonos, usando sempre o mesmo procedimento: recortamos os polígonos que queremos deduzir a fórmula da área, de modo a "montar" um retângulo, e assim, conseguiremos suas fórmulas de área, através da fórmula da área desse retângulo.
Faremos isso com um triângulo, um paralelogramo, um losango e um trapézio.

Com essa mesma brincadeira de recortes podemos sempre recortar um polígono qualquer, claro que com certos critérios, de forma tal que com as peças obtidas podemos montar um quadrado.
Você consegue imaginar como? Sobre isso, visite a atividade Polígonos Equidecomponíveis.
