Paralelogramo

PARALELOGRAMO

Como transformar um paralelogramo em um retângulo? Movimente o ponto vermelho da figura e observe:

	Se quiser alterar o formato do paralelogramo, movimente os pontos azuis. Para mormar um retângulo "diferente" rotacione a peça com o ponto preto. A Animação Java funciona melhor no navegador Internet Explorer.

Intuitivamente podemos nos convencer que as peças que compõem o paralelogramo se encaixam perfeitamente na composição do retângulo. O critério de construção das peças é:
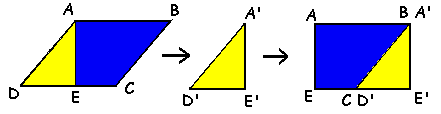
no paralelogramo temos a reta AE, perpendicular ao lado CD, passando pelo ponto A, formando o triângulo retângulo ADE. O triângulo congruente recortado A'D'E' encaixa-se, conforme indicam as cores, formando o retângulo ABE'E.
Devemos mostrar que a região triangular recortada do paralelogramo realmente se encaixa de modo a formar o retângulo. Veja a demonstração:
A partir do paralelogramo dado ABCD, construímos um retângulo ABXE, sendo X o ponto de intersecção da reta CD com a reta perpendicular a CD que passa por B. Traçamos o segmento AE, sendo E o ponto de intersecção da reta perpendicular a CD que passa por A. O triângulo AED é o triângulo recortado A'E'D'. Devemos mostrar que os dois triângulos (AED e BXC) são congruentes. De fato isto acontece:
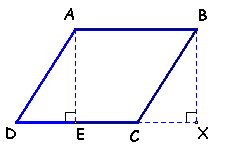
Os triângulos AED e BXC congruentes pois: os lados AD e BC são congruentes já que são lados opostos de um paralelogramo os ângulos ADE e BCX são ângulos correspondentes formados por uma transversal (CD) em duas paralelas (AD // BC) *os ângulos AED e BXC são retos Assim, o triângulo AED que recortamos (e chamamos de A'E'D') encaixa-se perfeitamente no triângulo BXC, formando o retângulo ABXE.

Agora que já está comprovado que podemos transformar um paralelogramo em um retângulo conservando a área, para deduzir a fórmula da área do paralelogramo a partir da fórmula da área do retângulo, só precisamos comparar os elementos relacionados:

Visto que
Aret = bret . hret
brer = bpar
hret = hpar
Aret = btri . hpar

e como
Aret = Atri
podemos concluir que Atri
é dada pela formula:
A = b. h

Assim, conseguimos "justificar" a origem da fórmula da área de um paralelogramo partindo da conhecida fórmula da área de um retângulo.