Consideremos, agora, um
retângulo com lados de medidas racionais a
e b. Podemos escrever esses números
como duas frações 
e 
, com o mesmo
denominador q. Podemos, também, dividir
cada lado do retângulo em segmentos de comprimento 
.
O lado de medida a ficará decomposto
em p segmentos justapostos, cada um deles
medindo . Da
mesma forma, o lado de medida b ficará
subdividido em r segmentos iguais, de comprimento
. Traçando
paralelas aos lados pelos pontos de subdivisão, o retângulo
ficará subdividido em p . r quadrados
de lado .
Cada um desses quadrados unidades terá área 
:
:
,
que nos permite concluir que cada quadrado de lado
terá área ,
entendendo que a unidade de área foi igualmente distribuída
entre eles.
,
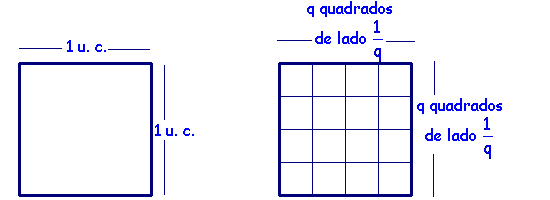
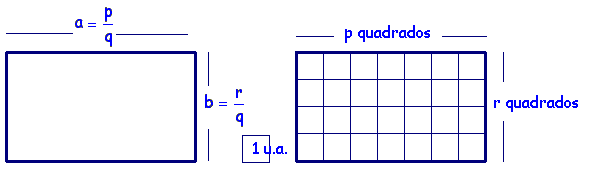
ou seja, ÁREAret = base x altura = a . b
Para mostrar que, mesmo no caso em que as medidas não são ambas racionais a fórmula continua válida, dividiremos o raciocínio em duas etapas:
1º) para
qualquer produto c . d <
a . b, veremos que c . d < ÁREAret;
2º) para qualquer produto a . b < e . f, veremos que ÁREAret < e . f.
Dessa maneira, veremos que ÁREAret não pode ser um número c . d menor nem um número e . f maior que a . b e portanto ÁREAret = a . b
2º) para qualquer produto a . b < e . f, veremos que ÁREAret < e . f.
Dessa maneira, veremos que ÁREAret não pode ser um número c . d menor nem um número e . f maior que a . b e portanto ÁREAret = a . b
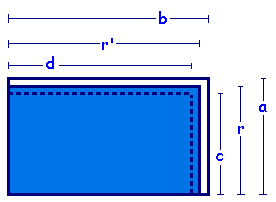
Como c . d < r . r', temos que
c . d < r . r' < ÁREAR
c . d < r . r'< a . b.
Dentro do retângulo R, desenhamos um outro retângulo de lados r e r' e área r . r' (conforme a fórmula acima). Temos que r . r' é menor que a ÁREAR, visto que o retângulo de lados r e r' está dentro do retângulo R de lados a e b.
Sabendo que c . d < r . r', temos que c . d < ÁREAR.
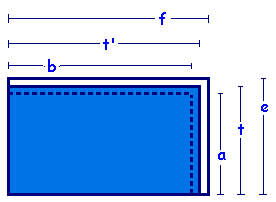
Como a . b < e . f, temos que
ÁREAR < t . t' < e . f
a . b < t. t' < e . f.
Fora do retângulo R, desenhamos um outro retângulo de lados t e t' e área t . t' (conforme a fórmula acima). Temos que t . t' é maior que a ÁREAR, visto que o retângulo de lados t e t' está fora do retângulo R de lados a e b.
Sabendo que e . f > t . t', temos que e . f > ÁREAR.
Assim, a ÁREAret
não pode ser nem maior nem menor que a .
b: ÁREAret = a . b , onde a
e b são números reais.
