Trapézio

TRAPÉZIO

Como transformar um trapézio em um retângulo? Movimente os pontos vermelhos da figura e observe:

	Se quiser alterar o formato do trapézio, movimente os pontos azuis. A Animação Java funciona melhor no navegador Internet Explorer.

Intuitivamente podemos nos convencer que as peças que compõem o trapézio se encaixam perfeitamente na composição do retângulo. O critério de construção das peças é:
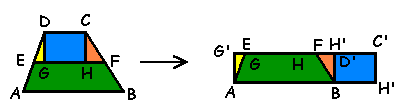
no trapézio temos a reta EF passando pelos pontos médios dos lados AD e BC, e os segmentos DG e CH perpendiculares a esta reta. Conforme indicam as cores, usando o trapézio ABFE, os triângulos EGD e FHC e o quadrilátero CDGH, construímos um retângulo com a mesma área do trapézio.
Sendo a nossa abordagem dentro do espírito da geometria dedutiva devemos mostrar que as regiões triangulares e quadrilátera que completam o retângulo obtido a partir do trapézio são de fato congruentes aos triângulos e ao quadrilátero que fazem parte do trapézio dado. Veja a demonstração:
Sobre o trapézio dado ABCD, construímos um retângulo com base igual a soma das bases do trapézio e o lado paralelo à base passando pelos pontos médios de AD e BC. Traçamos os segmentos DG e CH perpendiculares às bases do trapézio (e também, a EF). Devemos mostrar que os dois triângulos e o quadrilátero no trapézio dado são congruentes aos triângulos e ao quadrilátero pontilhados do retângulo, respectivamnete. De fato isto acontece:
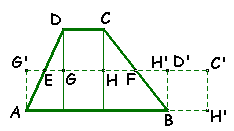
1.Os triângulos DEG e AEG' são congruentes pois: os lados DE e AE são congruentes já que E é ponto médio de AD os ângulos EGD e EG'A são retos os ângulos DEG e AEG' são congruentes já que opostos pelo vértice 2.Com raciocínio análogo mostra-se que também são congruentes os triângulos CFH e BFH'. 3.Os quadriláteros CDGH e C'D'BH' são congruentes pois: visto que ambos são retângulos (construídos com os quatro ângulos retos), têm os lados opostos congruentes o lado BH' foi construído congruente a CD, de forma que C'D'=GH=CD=BH' os lados DG e D'B são congruentes já que são paralelas entre si e perpendiculares a outro feixe de paralelas (CD\|\|EF\|\|AB) Assim podemos concluir que as peças que compõem o triângulo ABC se encaixam perfeitamente no retângulo construído.

Agora que já está comprovado que podemos transformar um trapézio em um retângulo conservando a área, para deduzir a fórmula da área do trapézio a partir da fórmula da área do retângulo, só precisamos comparar os elementos relacionados:

Visto que
Aret = bret . hret
brer = Btra + btra
hret =
Aret = (Btra + btra) .

e como
Aret = Atra
podemos concluir que Atra
é dada pela formula:

Assim, conseguimos "justificar" a origem da fórmula da área de um trapézio partindo da conhecida fórmula da área de um retângulo.