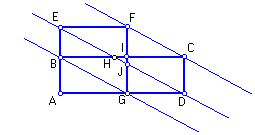
DEMONSTRAÇÃO

Sobrepomos o quadrado ao retângulo e traçamos as retas FC, ED e BG. Nosso objetivo principal é demonstar a congruência dos pares de triângulos GDJ e BHE, e DCH e JFE.
Como estamos admitindo que a base do retângulo é menor que o dobro da base do quadrado, a reta ED intercepta o lado do quadrado no interior do retângulo.
Os triângulos sobre os quais queremos mostrar congruências, são todos do tipo retângulo. Visualmente temos na figura diversos paralelogramos, os quais vão nos garantir congruências entre catetos dos triângulos. Assim basta mostar que de fato existem estes paralelogramos.

Da igualdade de áreas temos AB.AD = AE.AG, e portanto AD/AG=AE/AB. Disto concluímos que as retas BG e ED são paralelas, e portanto BEJG e GBHD são paralelogramos, usando-se aqui a caracterização de paralelogramo em termos de lados opostos paralelos.
Também temos que FJDC é paralelogramo.

De fato: sendo BEJG paralelogramo, temos EB e JG congruentes, e como EB é congruente à FI segue, por transitividade, que FI é congruente à JG. Temos então FJ congruente à IG, e consequentemente, congruente à CD, o que nos permite concluir que FJDC também é paralelogramo, usando-se aqui a caracterização de paralelogramo em termos de par de lados opostos paralelos e congruentes.

Sendo FJDC paralelogramo concluímos que são paralelas as retas ED e FC, e portanto EFCH também é paralelogramo tem par de lados opostos paralelos).
Da existência destes quatro paralelogramos concluímos que são congruentes os segmentos:
*GD e BH , BE e GJ , e portanto são congruentes os triângulos GDJ e BHE;
*DC e JF , CH e FE , e portanto são congruentes os triângulos DCH e JFE.


Volata para Retângulo Transformado em Quadrado