De Retângulo Para Quadrado

TRANSFORMAÇÃO DE RETÂNGULO EM QUADRADO

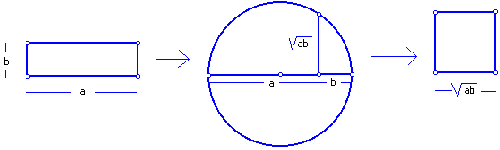
Para realizar esta transformação inicialmente construímos um quadrado com a mesma área do retângulo. Isto é feito usando-se régua e compasso:
*alinhamos dois segmentos de comprimentos a e b, iguais a base e altura do retângulo; traçamos círculo com centro no ponto médio dos segmentos alinhados; na extremidade comum aos dois segmentos traçamos segmento perpendicular ao diâmetro, até encontrar o círculo. Este segmento tem como medida a raíz quadrada de a.b, que é a medida do lado do quadrado desejado. (ver demonstração)

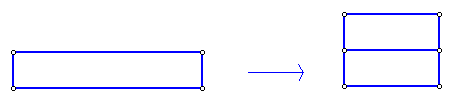
Feita esta construção, vamos transformar o retângulo em quadrado. Se o lado do retângulo é maior que o dobro do lado do quadrado, cortamos sucessivamente o retângulo em retângulos menores congruentes e "empilhamos" estes, de modo a formar um novo retângulo. Isto para que, mais adiante, os recortes funcionem bem:

Tendo um retângulo com lado menor que duas vezes o lado do quadrado de mesma área, a figura abaixo nos indica os recortes a serem feitos: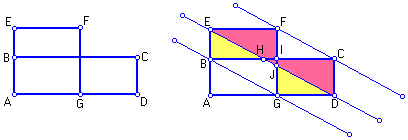

A construção feita é a seguinte:
*sobrepomos o quadrado ao retângulo e traçamos as retas FC, ED e BG
*as cores nos indicam os recortes a partir dos quais obtemos a transformação.

Como antes, intuitivamente podemos nos convencer que as peças recortadas no retângulo se encaixam perfeitamente no quadrado. Formalmente, devemos mostrar as congruências entre os pares de triângulos GDJ e BHE, e DCH e JFE. Para ver a demonstração clique aqui.