Discussão
do Modelo
| A atividade consiste em dado o modelo completo (com animações, gráficos e tabelas) de um jogador de basquete arremessando uma bola ao cesto, tentar reconstruir este modelo, aceitando-se adaptações que os alunos e o professor julgarem convenientes. | 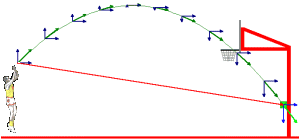 |
"Que tipo de trajetória a bola descreve? Mostre porquê. Como é o gráfico das componentes vertical e horizontal da posição da bola em função do tempo? Por quê? Dados a velocidade inicial, o ângulo de arremesso e a aceleração da gravidade, qual é a altura máxima atingida pela bola durante o movimento? Como é o gráfico das componentes horizontal e vertical da velocidade da bola em função do tempo? Por quê?".
| A construção do
modelo permite que se varie a posição da cesta em relação ao jogador.
Os parâmetros envolvidos são a velocidade inicial da bola ( |
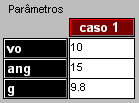 |
 |
 |
 |
A bola será tratada como uma partícula, portanto desconsideraremos possíveis efeitos de vibração, rotação e deformação da mesma. Além disso, o movimento da bola é dado segundo um plano vertical em relação ao solo.
| |
( 1 ) |
| ( 2 ) |
onde v e r
são os vetores velocidade e posição, respectivamente, da partícula no
instante t, 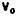 e
e 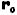 são os vetores velocidade inicial e posição inicial da partícula, respectivamente,
a é o vetor aceleração (constante) da partícula e t é o
tempo.
são os vetores velocidade inicial e posição inicial da partícula, respectivamente,
a é o vetor aceleração (constante) da partícula e t é o
tempo.
Como as equações ( 1 ) e ( 2 ) são vetoriais, podemos decompô-las segundo os eixos X e Y, com o sentido positivo do movimento da esquerda para a direita no eixo X e de baixo para cima no eixo Y. Escolhemos, por comodidade, a origem do referencial como a posição inicial da partícula. Desta escolha resulta que as posições iniciais (no plano cartesiano) são
Vejamos como ficam as equações ( 1 ) e ( 2 ) segundo os eixos X e Y:
|
|
Segundo
X
|
 |
Segundo
Y
|
|
|
( 1.a )
|
|
|
(
1.b )
|
|
|
(
2.a )
|
|
|
(
2.b )
|
A aceleração se dá
apenas segundo o eixo Y e tem sentido contrário ao convencionado,
assim 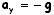 e
e 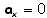 .
.
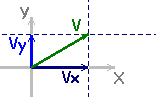
A velocidade no instante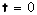 é
é 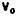 e faz um ângulo
e faz um ângulo 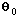 com o sentido positivo do eixo X.
com o sentido positivo do eixo X.
As componentes de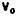 segundo X e Y são
segundo X e Y são 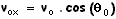 e
e 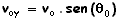 .
.
Fazendo-se as devidas substituições em (1.a) e (1.b), obtemos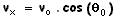 e
e  .
.
Ou seja, a componente horizontal da velocidade é constante ao longo de todo o movimento e a componente vertical varia linearmente com o tempo (função decrescente - por quê?).
O módulo do vetor velocidade em qualquer instante é dado por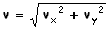 e o ângulo que o vetor velocidade faz com a horizontal é
e o ângulo que o vetor velocidade faz com a horizontal é  .
.
As componentes do vetor posição da partícula segundo os eixos X e Y são dadas, respectivamente, por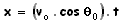 e
e 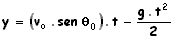 .
.
Combinando-se estas duas equações (lembrando que o tempo é elemento comum e igual) obtemos
A velocidade no instante
As componentes de
Fazendo-se as devidas substituições em (1.a) e (1.b), obtemos
Ou seja, a componente horizontal da velocidade é constante ao longo de todo o movimento e a componente vertical varia linearmente com o tempo (função decrescente - por quê?).
O módulo do vetor velocidade em qualquer instante é dado por
As componentes do vetor posição da partícula segundo os eixos X e Y são dadas, respectivamente, por
Combinando-se estas duas equações (lembrando que o tempo é elemento comum e igual) obtemos