modelo

Implementação do modelo

Agora vamos implementar o modelo do lançamento no Modellus. Para isso, temos um roteiro de sugestão:

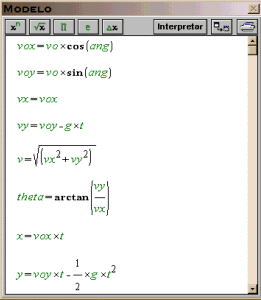
1. Escreva todas as equações na janela Modelo, cuidando para que a sintaxe esteja correta, de acordo com a linguagem do software.


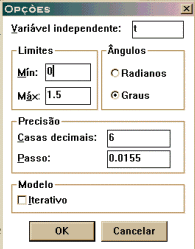
	2. Em opções da janela Controlo, mantenha t como variável independente. Determine os Limites Mín: 0 e Máx: 1,5. Marque para que os ângulos sejam marcados em graus. Na precisão, coloque 6 no item casas decimais e no item passo 0,0155.

3. Abra uma nova janela de animação.

4. Importe a figura do jogador de basquete, disponível na pasta imagens do Modellus; o nome da figura do jogador é basketm.bmp.

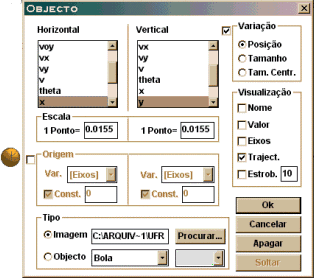5. Crie um objeto do tipo imagem importando a figura da bola de basquete (bolab1m.bmp)disponível na pasta imagens. Ative a visualização trajetória. Determine uma escala de 1 : 0,0155 nos dois eixos (por quê?).

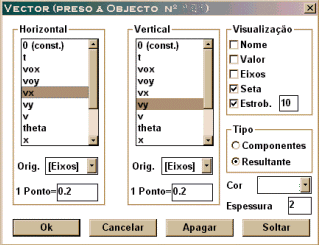
6. Crie o vetor posição da partícula escolhendo na Visualização: Seta. Determine uma escala de 1 : 0,0155 e selecione na Orig. [Eixos]. A cor e a espessura escolha a seu gosto (experimente vários casos). Marque como Tipo: Resultante.
7. Crie vetor velocidade da partícula. Escolha na Visualização: Seta e Estroboscópica de 10 em 10. Selecione como Tipo: Componentes. Na Orig. escolha [Eixos]. Faça uma escala de 1 : 0,2. Escolha a espessura e a cor e amarre o vetor à bola.
8. Crie novo vetor velocidade, só que agora do Tipo Resultante. Amarre o vetor à bola.

Verifique mais tarde que o vetor velocidade é tangente à trajetória da partícula (por quê?).

9. Você pode inserir os valores de x, y e theta na janela de animação para poder acompanhar sua variação no decorrer do modelo.

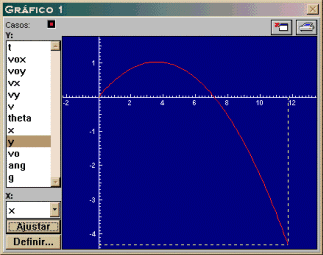10. Crie um novo gráfico para visualizar como variam a velocidade, a altura, o alcance horizontal, etc. em função do tempo.
Na figura ao lado temos o gráfico da trajetória da bola; para obter o gráfico de, por exemplo, como a velocidade varia em função do tempo selecione no campo y o v e no campo x o t.

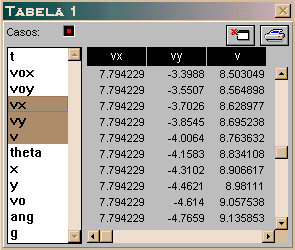
13. Crie nova tabela para poder verificar os resultados numericamente.

Você pode criar no Paint Brush a figura de uma tabela de basquete, obedecendo uma escala, e colar na janela de animação. Também pode acrescentar um texto explicativo ao modelo.

Agora, você está pronto para responder às várias questões lançadas durante essa atividade e também formular outras! Assim, estudar Modelos Matemáticos pode desenvolver mais raciocínio do que habilidade em algoritmos!