Teorema
2: Duas pirâmides de mesma base e mesma altura
têm o mesmo volume.
Para demonstrar esse teorema,
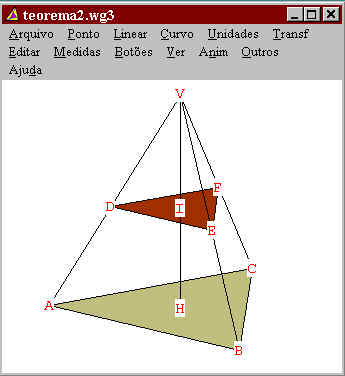
analisaremos o que ocorre quando uma pirâmide é seccionada por um plano paralelo a sua base.
|
Temos que DEF é paralelo a ABC, onde VI é a altura da pirâmide DEFV e
VH é a altura da pirâmide ABCV.
Daí temos dois fatos
importantes:
-
A seção e a
base da pirâmide são figuras semelhantes e a
razão de semelhançaa é (VI)/(VH).
-
A razão entre
áreas de figuras semelhantes é o quadrado da
razão de semelhança.
|
|
Com esses dois itens
demonstraremos o Teorema acima citado.
|
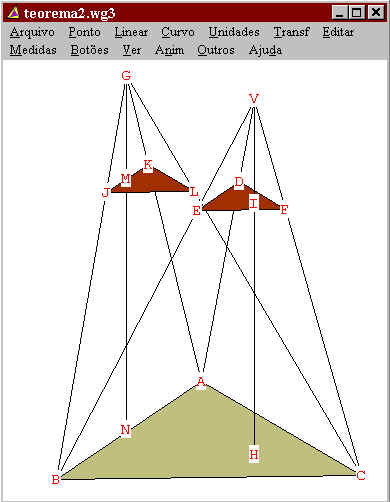
As pirâmides foram
construída de tal forma que G e V estão a mesma
distância do plano determinado pelo triângulo ABC (VH =
GN). As seções JKL e EDF estão a mesma distância do
plano ABC, ou seja GM = VI.
Seja A área
da base ABC e A1 e A2 as áreas das seções JKL e EDF.
Pelos itens citados acima, temos que:
(A1/A) = (VI/VH)2 =
(A2/A)
Temos então que
A1 = A2.
Usando Princípio de Cavalieri, que diz que se qualquer plano
horizontal secciona dois sólidos segundo figuras planas
com áreas iguais, então os dois sólidos tem o mesmo volume, concluímos
que os volumes das duas pirâmides são iguais, como queríamos demonstrar.
|
 |
Voltar
|

