|
(*)Ricardo Ribeiro
Aprendemos
no Ensino Médio que a fórmula do volume da pirâmide é igual a um
terço do produto da área da base (A)
pela altura (h).
V = (A.h)/3
Com o auxílio do programa Wingeom, demostraremos1 essa igualdade, mostrando que o volume da pirâmide é igual a um terço do volume de um
prisma de mesma base e mesma altura.
Para fazer download do arquivo no Wingeom clique
aqui.
Para fazer o download do programa vá em Software.
Precisaremos de dois Teoremas para auxiliar a nossa
demonstração:
Teorema 1: O volume de um prisma
regular é igual ao produto da área da base pela altura.
Teorema 2: Duas pirâmides de mesma base e mesma
altura têm o mesmo volume. (demonstração)
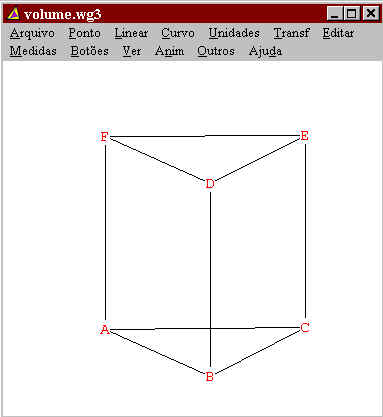
Para facilitar a visualização, utilizaremos um prisma
reto de base triangular para realizarmos a nossa
demonstração.
|
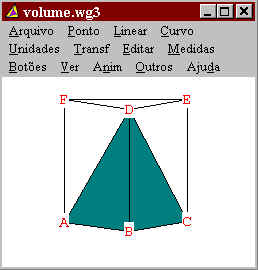
|
Seja A a área do triângulo ABC e seja h
a altura do prisma. Pelo Teorema 1 citado acima, sabemos que
seu volume é Ah.
Agora dividiremos esse prisma em três tetraedros (pirâmide de base triangular).
Mostraremos que os três tetraedros terão a mesma área da base e a
mesma altura, logo pelo Teorema 2, terão o mesmo volume.É claro que a soma dos volumes desses três tetraedros é igual ao
volume do prisma. |
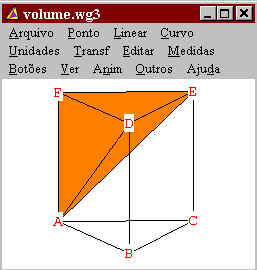
Seja V1 o volume do tetraedro definido pelo triângulo ABC e pelo vértice
D, V2 o volume do tetraedro definido pelo triângulo FDE e pelo vértice
A e V3 o volume do tetraedro definido pelo triângulo ACE e pelo vértice
D.
|
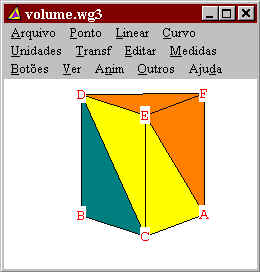
Ao lado temos o prisma composto pelos três
tetraedros. |
|
Note que o tetraedro verde é igual ao laranja, logo possuem o
mesmo volume.
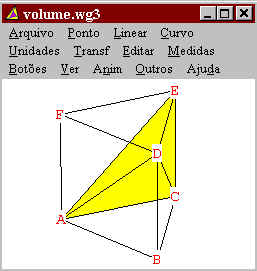
Agora falta mostrar que o volume do tetraedro amarelo é igual ao dos
outros dois. Para isso, utilizaremos o Teorema
2.
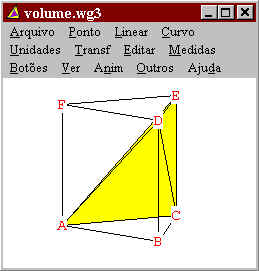
Por construção, temos que o segmento DB é paralelo a face ACE.
Logo a distância de qualquer ponto do segmento DB a face ACE é sempre a mesma.
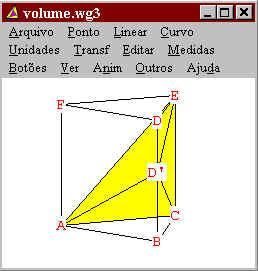
Imagine agora um ponto sobre o segmento DB, chamemos de D'. Agora imagine um
tetraedro formado pela face ACE e pelo vértice D'. Note que quando D'
for igual a D teremos o tetraedro inicial, e que quando D' for igual a
B teremos um tetraedro igual ao tetraedro laranja e verde. |
|
|
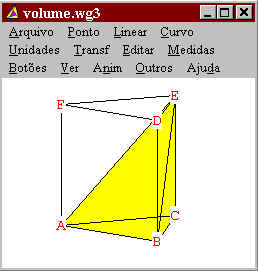
Como a distância de D, D' e B até a face
AEC é a mesma, temos, pelo Teorema 2,
que os dois tetraedros acima e o tetraedro ao lado tem o mesmo volume. Portanto o tetraedro amarelo
inicial tem o mesmo volume que os tetraedros verde e laranja.
Logo cada um dos tetraedros tem volume
igual a um terço do prisma, como queríamos demonstrar. |
|
Atividades Diversas
(*)
Aluno do curso de Licenciatura em Matemática da UFRGS/IM, orientado
pela professora Maria Alice Gravina
1Utilizamos
o livro A Matemática do Ensino Médio, Volume 2 de Elon Lages para
auxiliar a nossa demonstração. |