|
|
|
|
|
|
|
|
|
|
|
ATIVIDADES
GUIADAS |
|
|
|
|
|
|
|
|
|
|
SHAPARI
- Uma visão geométrica
diferente das transformações matriciais
|
|
|
Observe
que, se convencionarmos que todos os segmentos do plano tem início
na origem, ou seja, no ponto (0,0), poderemos identificar os segmentos
apenas pela sua extremidade. Por exemplo, o segmento que vai da origem
até o ponto (1,0) será identificado como segmento (1,0),
o segmento que vai da origem até o ponto (1,1) será identificado
como segmento (1,1) e assim por diante.
A
matriz de transformação A informa essencialmente como estão
sendo transformados os segmentos (0,1) e (1,0). Estes segmentos estão
desenhados no sistema de coordenadas abaixo:
|
|
|
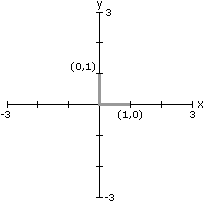 |
|
|
|
|
|
|
|
Se aplicarmos a matriz de transformação A a estes segmentos,
poderemos ter uma idéia exata do que acontecerá com a figura
inteira. Observe:
|
|
|
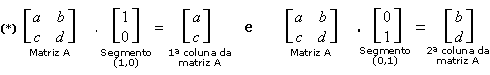 |
|
|
Você pode notar que aplicando a transformação A ao
segmento (1,0) temos como resultado exatamente a 1ª coluna de A,
e aplicando a transformação A ao segmento (0,1) temos como
resultado exatamente a 2ª coluna de A.
|
|
|
Exemplo
1
: A matriz de cisalhamento de fator k na direção x é:
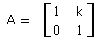
|
|
|
Como vimos em (*) , a primeira coluna da matriz A representa
as novas coordenas do segmento (1,0) e a segunda coluna de A representa
as novas coordenadas do segmento (0,1). Graficamente, temos:
|
|
|
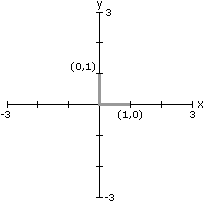 |
|
 |
|
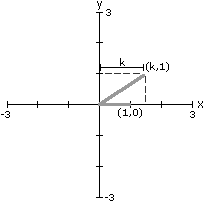 |
|
|
|
Exemplo
2 : A matriz de rotação é:
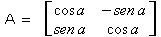
Logo,
as novas coordenadas do segmento (1,0) será (cosa, sena)
e do segmento (0,1) será (-sena,cosa). Graficamente
teremos :
|
|
|
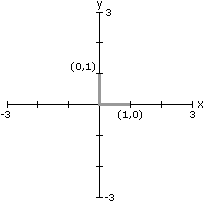 |
|
 |
|
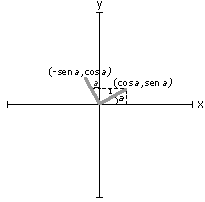 |
|
|
|
Esta interpretação pode ser feita para qualquer das transformações
que você já estudou e pode ajudar-lhe a imaginar como será
a matriz de transformação que você deverá construir
dependendo do resultado esperado. |
|
|
|
|
|
 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
 |



