Olhemos para algumas situações de nosso dia a dia:

• determinar a distância percorrida por um carro movendo-se com velocidade constante
• determinar o preço de certa quantidade de cadernos sabendo-se o valor unitário
• determinar o preço de um imóvel em função do CUB (custo de m² de construção).

• x = tempo e y = distância percorrida em função do tempo
• x = número de cadernos e y = custo total
• x = número de metros quadrados e y = custo total.

se o valor da variável independente "x" dobra, o mesmo acontece com o valor da variável dependente "y"; se o valor de "x" triplica, também triplica o valor de "y"; mais geralmente, se a variável "x" é multiplicada por um número natural "n", o mesmo acontece com a variável "y". Em outras palavras: o quociente "y/x" se mantém constante.

O conceito de função linear: Uma função que estabelece entre x e y uma relação tal que y/x é constante é dita linear. Expressamos a relação por y = a.x, "a" constante e dizemos que a variação de "y" é diretamente proporcional a variação de "x".

Vamos mostrar que o gráfico de y = a.x é uma reta, a saber a reta passando por O=(0,0) e A=(1,a).

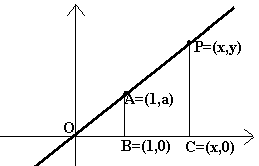Os pontos O=(0,0) e A=(1,a) estão no gráfico da função, pois suas coordenadas satisfazem a relação y = a.x. Seja P=(x,y) é um outro ponto qualquer neste gráfico. Os triângulos OPC e OAB são semelhantes porque ambos tem um ângulo reto e y/a = x/1 (lembre-se que y/x = a/1, já que P=(x,y) está no gráfico da função). Segue-se disto que os ângulos POC e AOB são congruentes, e como tem em comum o lado OC segue que P, A e O estão alinhados. Ou seja P está na reta passando por O e A.

Uma observação importante: nos exemplos apresentados acima as funções são crescentes e as variáveis envolvidas estão em relação de proporcionalidade direta. Vamos olhar para outras situações:

• Função crescente com variáveis que NÃO estão em relação de proporcionalidade direta:
  - O crescimento populacional em função do tempo.
  A medida que passa o tempo, a população de um país aumenta, mas não em proporcionalidade direta. Observe a tabela abaixo:
  
  

  ANOS	POPULAÇÃO (milhões)
  1940	40
  1950	50
  1960	70
  1970	93
  1980	119
  1990	150

  
  

  Para intervalos iguais de "anos", temos intervalos cada vez maiores de "população".
  
  

• Função decrescente e variáveis em relação de proporcionalidade direta:
  - Um exemplo para esse caso seria a reta y = -x. Fica a seu critério encontrar um exemplo prático do nosso dia-a-dia.

  ---

  Volta para Módulo III